古希腊哲学家芝诺提出过一个著名的悖论：希腊神话中的阿基利斯——一个以善跑著称的英雄，不能追上一个行动很慢的乌龟。他的具体论述如下：假定阿基利斯与乌龟沿着同一直线运动，乌龟在前，阿基利斯在后面追赶。不论阿基利斯跑的速度有多快，也无法追上乌龟。他的理由是：当阿基利斯到达乌龟的起点A时，乌龟在这段时间内又走到了A1点。而当阿基利斯追到A1时，乌龟又利用这一段时间跑到了A2，这样就得到了一串点列：A,A1，A2，…。当阿基利斯到乌龟上一次的起点An-1时，乌龟又利用这一段时间，从An-1向前慢慢移动到An。如此下去，阿基利斯将永远追不上乌龟。
线段AA1，A1A2，A2A3的长度按固定比例递减
我们该如何解释芝诺的悖论呢？问题出在哪里？
的确，在阿基利斯到达每一个点An时，他都落在乌龟之后，不管n有多大，都是如此。但是，阿基利斯“永远”追不上乌龟的结论不能成立。这是因为“永远”指的是时间，而n只是阿基利斯在追赶过程中没有追到乌龟之前的一串点An的编号而已。这个编号n可以任意大，完全不等于追赶时间要任意长。芝诺在讨论中偷换了概念。
古希腊哲学家芝诺
现在，让我们计算一下阿基利斯自起点追赶到An的时间。
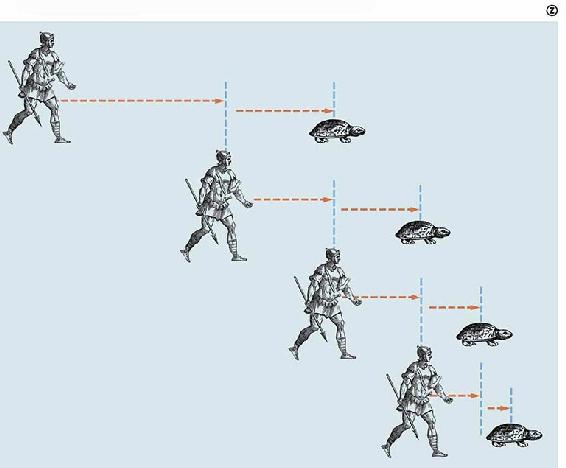
阿基利斯追到乌龟初始位置时，乌龟又向前跑了一段
设比赛开始时乌龟与阿基利斯之间距离为d，而乌龟与阿基利斯的速度分别是v与u。假定q为v与u之比，即q=v/u，那么q是小于1的正数。阿基利斯自起点到达乌龟的起点A时所需要的时间为t0=d/u，而在这一段时间内，乌龟从A走到A1，而A到A1的距离为
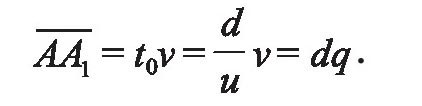
当阿基利斯自A走到A1，所需的时间为
而在t1这段时间内，乌龟又从A1走到A2，所走的距离为
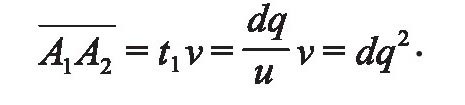
如此下去，用数学归纳法不难证明：An-1到An的距离是
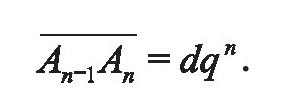
有了这些公式，我们就可以推出从A到An的距离为
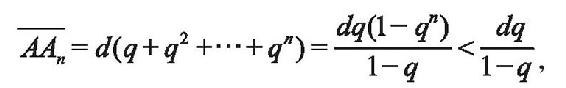
而阿基利斯自起点到An的总时间为
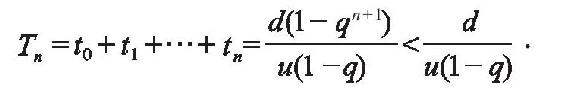
这里最后一个等式用到了等比数列的求和公式。
这样，无论n有多大，Tn不会超过一个固定的数
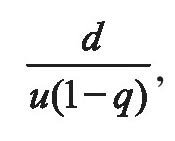而且容易看出，当n→∞时，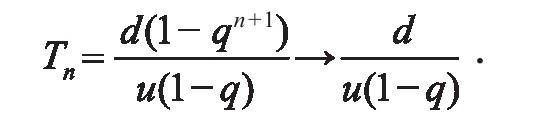
这就告诉我们，在阿基利斯追赶乌龟的过程中，总时间不会超过
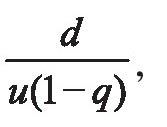怎么能说“永远”追不上呢？读者还不难验证，在阿基利斯追赶的时间达到
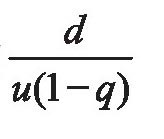时，他与乌龟恰好相遇。总之，在上述例子中，随着n的增大，线段An-1An按一个固定比例缩小，从而阿基利斯走完这段路程An-1An所需的时间也按固定比例缩小。因此，所花费的总时间是个有限数，并不是无穷。
奔跑的阿基利斯与乌龟
事实上，任何运动都是一个无限的过程。一个人从某一点走到另外一点，尽管所花的时间以及所走的距离都是有限的，但是运动的过程却是无限的，因为这个人必须走过无数个点才能到达目的地。这个过程的无限性不能推出所花的时间也是无限的。
一般说来，数学中的极限过程都是一个无限过程，但其极限值却是一个有限数。（李忠）
【微博士】芝诺悖论
芝诺（约前490—前430）是古希腊哲学家、数学家。他提出的一系列运动不可能性悖论世界闻名。现在人们熟知的芝诺悖论有十个，主要记录在亚里士多德的《物理学》一书中。其中最著名的有阿基利斯悖论和飞矢不动悖论。
阿基利斯悖论：阿基利斯永远追不上在他前面爬行的乌龟。当阿基利斯跑到乌龟最初所在位置时，乌龟又向前爬行了一段距离，已到达下一个位置；阿基利斯跑到乌龟的下一个位置时，乌龟又向前爬了一段距离，如此下去，阿基利斯永远无法追上乌龟。
飞矢不动悖论：飞行中的箭是不动的。因为时间是由瞬间组成的，飞行中的箭在每个瞬间都是静止的。
【微问题】你能解释“飞矢不动”悖论吗？
【关键词】芝诺悖论 极限
- 免疫系统是如何工作的？
- 兔子的耳朵为什么这样长?
- 兔子的长耳朵有什么作用
- 全世界共有多少座核电站？
- 全国名老中医药专家周乐年:慢病延年的补养之道
- 全息照相与普通照相有什么不同
- 全球变暖可能消失一半物种
- 全球变暖威胁尼泊尔冰川湖
- 全球变暖导致北极池塘蒸发作用增强
- 全球变暖将使美国东北部受到毁灭性打击
- 全球变暖，为什么太平洋小岛国最着急
- 全球定位系统是什么？它又是如何运作的？
- 全球性断裂网格
- 全自动洗衣机是怎样把衣服洗干净的
- 八卦和五行有什么关系
- 八哥为什么喜欢站在牛背上
- 八哥在水牛背上啄什么?
- 八旗制度是怎样建立的?
- 八月十五的月亮最圆吗
- 八棱海棠的栽培技术是怎样的
- 八目鳗真的有八只眼睛吗?
- 公众号写文心得体会:你看,这是干货吗
- 公共汽车的门为什么能自动开关
- 公猫趁老婆不在家,偷上了其他小母猫
- 公认的植物学创始人是谁？