一张纸有正反两面，正面写满了字，反面还可以写。一般来说，常见的曲面也大都有正反两面，比如像足球一样的球面有外面和里面，救生圈一样的环面也有外面和里面，竹筒一样的圆柱面也有外侧和内侧。看上去所有的曲面都是有正反两面的。
情况是不是这样呢？让我们来做个实验。先裁出一张长方形的纸条，这张纸条当然是有正反面的。将纸的一端扭转180°，然后将这一端的正面和纸条另一端的反面粘合，粘成一个拧着的纸圈，这样一个纸圈就没有正反面了，它只有一个面。
德国数学家莫比乌斯
这个纸圈是由德国数学家、天文学家莫比乌斯首先发现的，称为莫比乌斯带。读者可能会奇怪，莫比乌斯带怎么会只有一个面呢？把纸圈拿起来，两个手指接触的不就是它的正反两面么？为此，我们先得理解什么是曲面的两个面。按通常方法粘成的纸圈（不经过扭转180°），如果给这样的纸圈涂上颜色，我们可以连续地（即刷子不离开纸面）给纸圈的一侧涂满一种颜色，但不越过纸的边界就不能涂刷到纸圈的另一侧，或者我们可以在纸圈的另一侧涂刷上另一种颜色。这样可以用颜色来区分纸圈的正反两面，即两种颜色分别代表了纸圈的两个不同的面，颜色相同的地方在同一面，不同的在不同面。这样涂色对球面、环面、平面等均同样有效。现在我们对莫比乌斯带也进行涂色，马上可以发现，用一种颜色就可连续地将整个莫比乌斯带涂满而不留一点空白，无法再涂刷上另一种颜色了。也就是说，莫比乌斯带的每个地方都是同一种颜色，这就说明了它只能有一个面，是一个单侧曲面。
再循环标志
当我们用两个手指，比如拇指和食指，拿起通常方法粘成的纸圈时，我们可以确定拇指接触的是正面，食指接触的是反面。但对莫比乌斯带，如果我们也指定拇指接触的是正面、食指接触的是反面，就会出现问题。因为如果这种指定是合理的话，让手指在莫比乌斯带上移动时，拇指接触的应该永远是正面，但当手指沿莫比乌斯带移动一圈回到开始的位置时，我们发现，拇指现在接触的地方正是开始时食指接触的地方，即原来确定为反面的，现在又要确定为正面，因此这样的曲面就无法确定正反面了。数学上称这种可以指定正反面的曲面为可定向曲面，而不可指定正反面的曲面为不可定向曲面。可定向曲面有正反两个面，而不可定向曲面只有一个面。
莫比乌斯带
莫比乌斯带还有很多奇特的性质。通常的纸圈有两条边，而莫比乌斯带不但只有一个面，还只有一条边；如果将莫比乌斯带沿中线剪开，得到的不是两个分开的纸圈，而是一个两倍长的拧着的纸圈（但这个纸圈是可定向的），再将这个纸圈沿中线剪开，得到的是两个相互扣着的纸圈。莫比乌斯带的奇妙特征，常被用于设计成各种标志，比如再循环标志就是利用了莫比乌斯带循环往复的几何特征，从莫比乌斯带演化而来。2010年上海世博会湖南馆也设计成了莫比乌斯带。
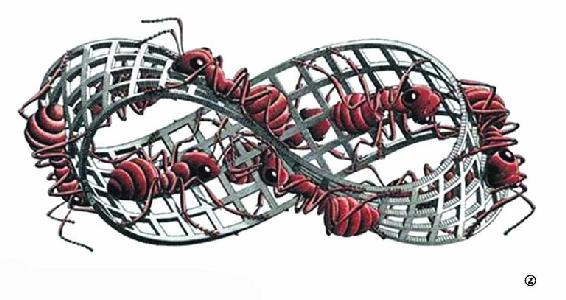
埃舍尔作品《莫比乌斯带Ⅱ》
那么，莫比乌斯带又有什么用呢？除了数学上的意义外，其特殊的性质还有许多实际用途。比如，将奥运奖牌的带子设计成莫比乌斯带，奖牌就能平服地贴在胸前，一些胸卡的带子也是这么设计的。将传送带设计成莫比乌斯带，则整个传送带就可均匀地承受磨损，避免普通传送带单面磨损的情况，延长使用寿命。打字机的色带也设计成莫比乌斯带，这样可以充分利用色带的整个表面。环绕式录音磁带设计成莫比乌斯带，可成倍增加录音和播放时间。利用莫比乌斯带的特性，还可以设计出无感电阻、莫比乌斯共振器等电子器件。
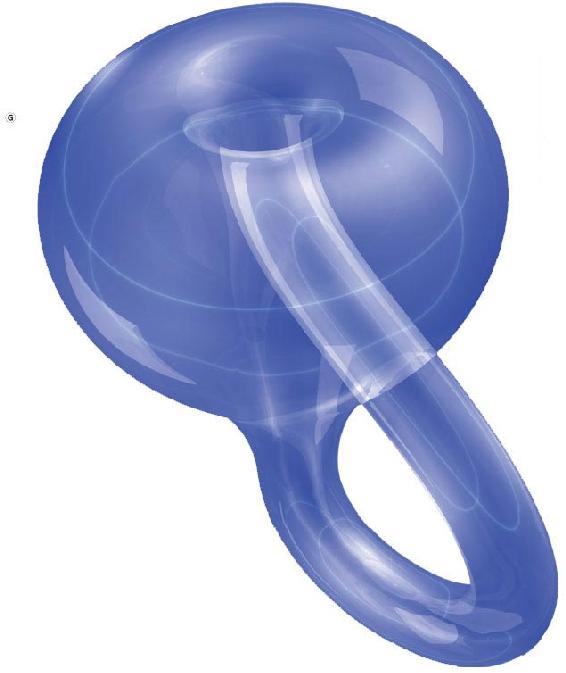
克莱因瓶
莫比乌斯带是一个有边的单侧曲面，那么是否有像球面或者环面那样封闭的无边的，且只有一个面的曲面呢？这样的曲面也是可以构造出来的。我们知道莫比乌斯带只有一条边，一个圆盘也只有一条边，将一条莫比乌斯带的边和一个圆盘的边粘合起来就可得到一个封闭的无边曲面。这个曲面也只有一个面，数学上称为射影球面。一只在这个曲面“内部”的小虫沿着莫比乌斯带走一圈，不用穿过曲面就能跑到这个封闭曲面的“外部”来，很奇怪吧？不过你不要真的去粘合一条莫比乌斯带和一个圆盘，因为这在我们生活的三维空间里是无法做到的，要在数学家想象的四维空间中才能做到。此外，将两条莫比乌斯带的边粘合也可以得到只有一个面的封闭曲面，称为克莱因瓶。当然，这在三维空间里也是无法实现的。（邱维元）
2010年上海世博会湖南馆的曲面构造
【微问题】你还能从莫比乌斯带构造出哪些东西？
【关键词】莫比乌斯带 克莱因瓶
- 地球与太阳系中的其他行星的距离
- 地球为什么不发光?
- 地球为什么会有引力?
- 为什么人的眼睛长在脑袋前方
- 为什么人的耳朵不会转动?
- 为什么人的耳朵能听见各种声音?
- 为什么人的肤色会不一样?
- 为什么人的身体会有感觉
- 为什么人的身体可以动
- 为什么人的食物都来自其他生物
- 为什么人的鼻子可以闻到气味?
- 为什么人的鼻子远不如狗鼻子灵敏
- 为什么人睡着了会做梦
- 为什么人睡觉时会磨牙
- 为什么人类不能随心所欲地操纵天气
- 为什么人类会哭泣?
- 为什么人类会进化出悲伤和恐惧情绪
- 为什么人类天生怕蛇
- 为什么人类生育男女性别比例差不多?
- 为什么人类的脚印还留在月球上?
- 为什么人类离不开植物?
- 为什么人类能知道恒星的身世
- 为什么人类要探测深海
- 为什么人类要研制防振合金?
- 为什么人类需要睡觉？