别莱利曼是世界著名的科普作家，他的“趣味科学系列”图书一直畅销不衰。为了纪念他，月球背面的一座环形山就是以他的名字命名的。
在《趣味几何学》中，别莱利曼列举了大量关于测量的生动例子，尽管这些方法不是他首创的，但他把这些方法生动地介绍给了广大读者。下面就是一例。
如果面对一条比较宽的河流（假定是比较直的），没有很长的绳子，怎样既快又准地测量它在某处的宽度呢？
这需要一把“等腰直角三角尺”。假定你要测量的宽度两端是A和B,A是对边的一个地点，B是你站立的地方。当然能为A做个标记最好，比如一根木桩或一棵树之类，反正总是要记住A点的位置（但并不需要过河）。
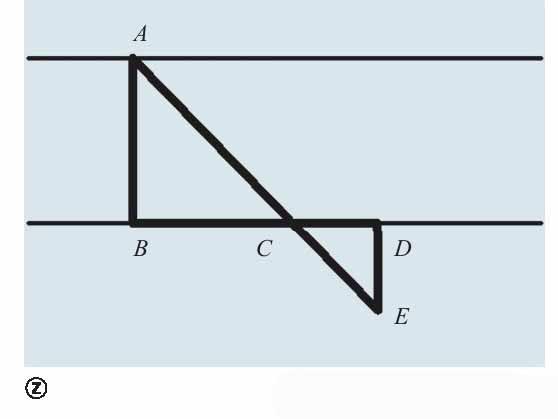
测量河流宽度示意图
然后再让三角尺的一直角边对准AB方向，这样另一直角边就定出了与这个方向垂直的方向BC，在B、C（C可任取）处各竖一根木桩，然后再在BC延长线上找一点D，用三角尺的一直角边对准BC方向，使得另一直角边与BA平行（当然是反方向，否则人要到水里去了），沿着这一方向走，找到一点E正好看不到A（也就是被C遮住，或E、C、A三点共线）。于是得到两个相似的直角三角形ABC和EDC。由简单的比例性质，有
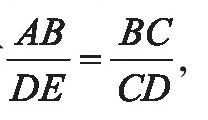于是分别测出DE、BC及CD，便知道河流的宽度AB了。有人肯定会问，既然CD是我们决定的，那么让BC=CD，此时两直角三角形全等，直接得出AB=DE，岂不更省事？这当然没错，但在现实中，比如河流较宽，有400米或1000米，那我们为了确定点E要走很远啊！这是很不合适的，所以实际情形也要考虑进去。（田廷彦）
【微博士】《海岛算经》中的一道题
在刘徽的《海岛算经》中有这样一道题目：今有望海岛，立两表（即竖直的标杆）齐，高三丈，前后相去千步，令后表与前表参相直（即两表与海岛顶峰处在同一平面内）。从前表却行（后退）一百二十三步，人目著地，取望岛峰，与表末参合（即眼睛、表的顶点、岛峰三点共线），从后表却行一百二十七步，人目著地取望岛峰，亦与表末参合，问岛高及去表（岛与前表距离）各几何？
尽管现在用相似和比例来做并不很困难，可在当时是很了不起的，也只有数学家才想得出。
【微问题】你能否试着测量一栋大楼的高度？
【关键词】测量 相似比 勾股定理
- 德国汽车文化之《发展的困惑》
- 德国瓦尔特PPX手枪
- 德国索尔恩霍芬采石场为何对古生物学如此重要？
- 德昂族有哪些礼仪和禁忌
- 德银是什么？
- 心悸有哪些症状_心悸需要做什么检查
- 心搏骤停时临床有哪些表现?
- 心理咨询师证书被取消后该怎么办:我选择了从0到1
- 心理咨询师证书被取消的五个问题
- 心理:自信与自恋有很大区别
- 心肌梗塞病人三大合并症?
- 心肌梗塞的症状有哪些呢
- 心脏为什么会永不停息地跳动
- 心脏为什么会跳个不停?
- 心脏为什么能不停的跳
- 心脏为什么跳个不停?
- 心脏和肺的本质关系是什么？
- 心脏是如何工作的？
- 心脏有多大，位于人体的哪个位置？
- 心脏杂音对人体健康产生哪些危害
- 心脏病的医学名称是什么？
- 心脏的功能
- 心脏起搏器与可植入除颤器有什么不同？
- 心血管堵塞的症状有哪些
- 心血管系统和循环系统有什么不同？