在所有的数列中，斐波纳契数列无疑是最著名的一个。1202年，生于意大利比萨的数学家莱昂纳多·斐波纳契完成了他的传世名著《算盘书》，书中对一个有趣的“兔子繁殖问题”进行了研究，斐波纳契数列便由此而来。
向日葵花盘中隐藏有斐波纳契数列
兔子繁殖问题实际上是斐波纳契提出的一个数学模型：假定一对大兔子一年生一对小兔子，一对小兔子一年后长成为一对大兔子，且所有的兔子都长生不死，那么这些兔子是按照什么样的规律繁殖的呢？
第一年，只有一对小兔子。第二年，小兔子长成为一对大兔子，兔子的对数还是1。
第三年，大兔子生出一对小兔子，兔子的对数变成2。
第四年，大兔子又生出一对小兔子，原来的一对小兔子长成为一对大兔子，兔子的对数变成3。
……
总结兔子的繁殖规律，可以发现：
每年的兔子对数=上一年的兔子对数+该年新生的兔子对数=上一年的兔子对数+上一年的大兔子对数=上一年的兔子对数+上上一年的兔子对数。
也就是说，如果记第n年的兔子对数为Fn，则F1=F2=1，且对n≥3，有Fn=Fn-1+Fn-2，于是便得到如下的数列：
1，1，2，3，5，8，13，21，34，55，89，144，233，377，610，987，…
其中从第三项起，每一项均等于前面两项之和。由于这个数列是由斐波纳契首先加以研究的，后人就将其称为斐波纳契数列。
斐波纳契数列是一个非常有趣、有用而且有名的数列，它有许多奇妙的性质，数学家对它的研究至今没有停止。下面我们简单介绍几项。
用斐波纳契数列的前六个数1，1，2，3，5，8为边长的6个正方形，可以拼成一个边长为8和13的矩形。
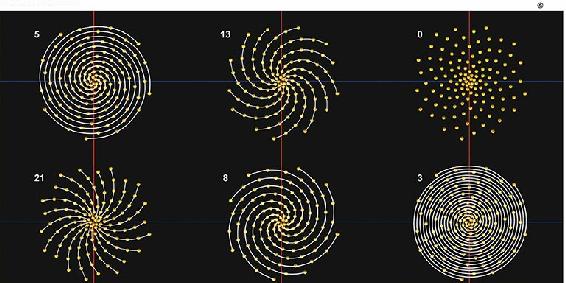
斐波纳契螺线
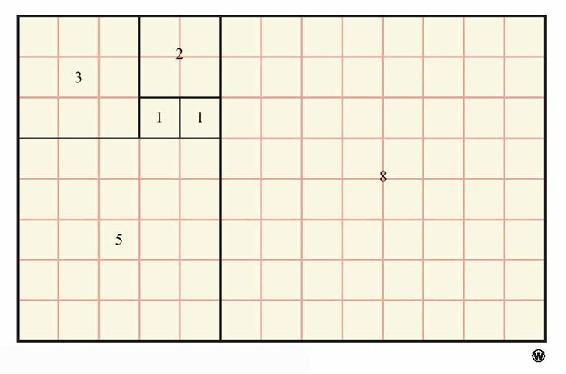
用斐波纳契数列前6个数拼成矩形
一般地说，以斐波纳契数列的前n个数为边长的n个正方形可拼成一个矩形，它的边长为Fn和Fn+1。实际上，可用数学归纳法证明下述性质：
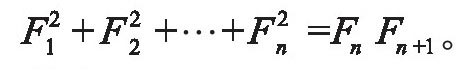斐波纳契数列还有通项公式：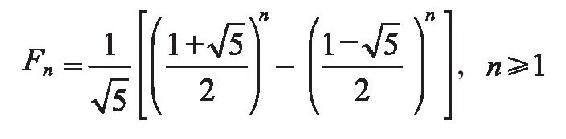
其中，
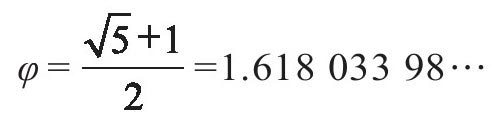就是著名的黄金分割。一个完全由自然数构成的数列，其通项公式竟然是由无理数φ来表示的，是不是很神奇呢。早在18世纪中叶，著名数学家棣莫佛和欧拉就已知道这个公式。到19世纪中期，法国数学家雅克·菲利普比内又重新发现了这一公式。
此外，可以看出的是，当n越来越大，斐波纳契数列中连续两项的比率Fn+1/Fn会越来越趋近于黄金分割φ。
除了许多数学上的奇妙性质以外，科学家还注意到，植物界中的某些数量分布也是遵循斐波纳契数列的，比如树枝分叉的数目、鲜花花瓣的数目、果实颗粒的分布、果皮螺纹的排列等。在美丽的向日葵上，其花盘上就有一左一右的螺旋线，如果有13条右旋，就有21条左旋，总数是34条。松果的鳞片也以螺旋状排列，小型的松果鳞片向右或向左排出5列，反方向则有8列，较细长松果的则是8列或13列。另外，许多植物的花瓣数目多为3、5、8、13、21等，有兴趣的话你可以找些花朵来数一数。
斐波纳契学会创始人、美国学者布鲁索正拿着一个大松果向学生讲述斐波纳契数列的性质
植物的叶子在茎上的排列呈螺旋形上升
植物的叶子在茎上的排列呈螺旋形上升。1611年，德国天文学家开普勒发现，如果把位于枝干或茎的周围的同一方向上的最近的两片叶子分别看成一个周期的开始和结束，在这个周期内可能有很多叶子，它们沿着枝干或茎也许会绕好多圈。记一个周期中叶子的总数为m，而这个周期中叶子所绕的圈数为n，则m与n都是与斐波纳契数列有关的数。例如，榆树的n=1，m=2；山毛榉的n=1，m=3；樱桃、橡树的n=2，m=5（也就是说，每个周期内有5片叶子，绕2圈才结束一个周期）；梨树的n=3，m=8；柳树的n=5，m=13。这些数都是斐波纳契数列中的数，实在是太神奇了！
关于斐波纳契数列的故事还有很多，特别是斐波纳契数列与黄金分割有密切关系。（李大潜 徐诚浩）
【科学人】莱昂纳多·斐波纳契
斐波纳契（1170—1250）是中世纪意大利最重要的数学家之一。他从小随父亲周游过很多地方，并在北非接受教育。1200年前后，斐波纳契回到比萨，撰写了一系列重要的数学教科书，其中最重要的当属《算盘书》（1202年）。这本书以斐波纳契在游历过程中积累的数学知识作为基础，其最重大的贡献是将印度和阿拉伯人所用的位值十进制系统和阿拉伯数字引入欧洲。书中有一个章节就是专门讲述斐波纳契数和斐波纳契数列的。
【微问题】你能推导出斐波纳契数列的通项公式吗？
【关键词】斐波纳契数列 黄金分割
- 叶绿体器官
- 号称“绿色陷阱"的沼泽是怎样形成的?
- 吃冰淇淋为什么要适量?
- 吃啥补啥的神奇
- 吃土豆要不要去皮?
- 吃完午餐之后为什么会感到困乏
- 吃巧克力:降了血压还缓解压力
- 吃核桃真的很补脑吗?
- 吃水果为什么不可以代替吃蔬菜?
- 吃水果有时间限制吗早上吃比晚上更营养?
- 吃水果要不要吃水果皮?
- 吃水泡饭为什么不好?
- 吃汤泡饭为什么不宜?
- 吃烤馒头为什么不好?
- 吃盐过多为什么有损健康?
- 吃米饭时嘴里为什么有甜味?
- 吃红薯为什么肚子胀?
- 吃红薯为什么肚子胀
- 吃肉、喝奶会致癌?
- 吃腐烂的食物,会中毒吗?
- 吃花胶补胶原蛋白吗?真相是:还不如吃鸡蛋!
- 吃荤的植物
- 吃药为什么分饭前饭后
- 吃药时碰到舌头的哪个部位最苦?
- 吃菠萝为什么要蘸盐水?