自然对数的底e=2.718281828…在数学中是一个重要的常数。为什么要引进这个常数呢？它有哪些重要应用？让我们细细道来。
首先来考虑一个理想状态的复利问题：设想有这样一家银行，它的年利率为1。一个客户年初以1元为本金存入，那么年终本利总和为1+1=2（元）。如果这家银行对期限更短的存款也采用同样的利率，即其利率根据存款期限在一年中所占比例按年利率打折计算，比如半年利率为1/2，三个月利率为1/4，一个月利率为1/12等。现在客户有更佳的存款策略：如果把1元钱存半年，到期立即连本带利续存。这样，年终的本利总和为
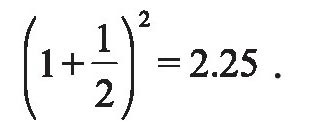
如果存期为3个月，到期后立即本利续存，则年终本利总和为
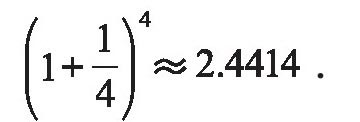
如果存期为1个月，则年终本利总和应该为
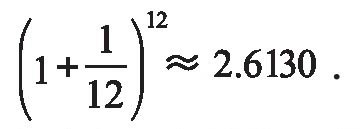
从这里可以看出，存款期限越短，按上面复利计算，年终所获得的本利总和越大。设想这家银行允许存款期限任意短，比如存期可以是1天、1小时或1分钟，甚至更短，那么存入1元1年后本利总和可以大到怎样的程度呢，存钱人会不会因此变成巨富呢？
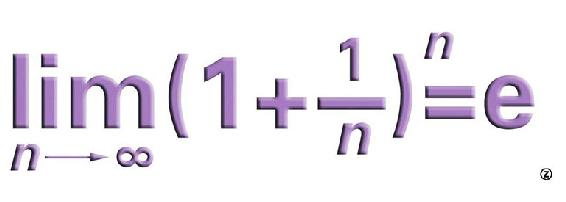
1697年，瑞士数学家雅各布·伯努利考虑了这个问题。把一年分作n等分，以
年为存期进行复利计算，那么一年后的本利总和为
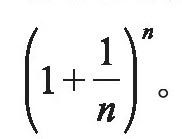雅各布·伯努利证明了当n越来越大以至于趋于无穷时，上面这个本利总和会越来越大，但不会无限增大，而会越来越趋近于一个固定的数值，这个值在2和3之间。现在知道这个值等于2.718281828…。用数学极限的术语来说就是：
1617年苏格兰数学家纳皮尔制作的计算装置，由1个底座和几根柱子组成，可把乘法运算转换为加法运算，把除法运算转换为减法运算
当n趋于无穷时，序列
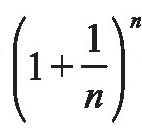的极限存在。这就告诉人们，无论客户怎样缩短存款期限，年终本利和不会超过这个数列的极限值2.718281828…。如果每时每刻都按复利计算，年终本利和就是这个极限值。
后来，瑞士数学家欧拉在研究指数函数与对数函数时，再次遇到了这个极限值，并把它记为e。他还证明了e是一个无理数。更重要的是，欧拉证明了对于任意的实数x，当n趋于无穷大时，数列
的极限为ex，即以e为底的指数函数。它恰好是前面复利计算例子的推广：本金依旧为1，但年利率改成x。在这样的条件下，如果每时每刻都按复利计算，到了年终本利之和就是ex。
不过，这里的“利率”x可正可负，为任意非零实数。
上述银行自然是一个虚构的数学模型，但确实有很多实际的自然现象符合这个模型。只要一个量每时每刻都按这个量的一个固定比率增加（或减少），那么这个量的变化就符合上面的指数增长（或减少）规律。比如，放射性物质的质量随时间衰变，声波或光波的强度随传播距离衰减，人类对各种刺激的反应和刺激强度之间的关系等，都符合上面的指数率。马尔萨斯关于人口指数增长的结论也是基于同样的数学模型得到的。
欧拉还证明了指数函数ex的瞬时变化率（即导数）就是它自己。举例来说，如果一个运动的物体在t时刻的速度是et，则在t时刻的加速度也是et。函数ex的这个独特性质，使得ex在微积分计算、求解微分方程等应用中扮演着特殊的角色，从而在各种理论推导以及工程计算中，不断地出现数e以及ex。
随着科技的进步与数学的发展，数e的用处越来越广泛。在数学的各个领域，数e的身影处处可见。其中重要原因就是以e为底的指数函数的独特性质。（李忠）
- 为什么鸭子的羽毛不会湿
- 为什么鸵鸟不会飞
- 为什么鸵鸟要把头埋进沙堆里
- 为什么鸽子树蜚(fěi)声中外?
- 为什么鸽子能从遥远的地方飞回自己的家
- 为什么鹅卵石那么光滑
- 为什么"鹞"式飞机能垂直起降?
- 为什么鹞式飞机能垂直起降?
- 为什么鹤会翩翩起舞
- 为什么鹤要用一只脚站着睡觉?
- 为什么鹦鹉可以说话?
- 为什么鹦鹉善于学人说话
- 为什么鹦鹉能模仿人说话
- 为什么鹭站在水中一动不动?
- 为什么鹭鸟的粪便是白色的
- 为什么鹭鸶、鹤等鸟类常常用一只脚站立着
- 为什么鹭鸶、鹤等鸟类常用一只脚站立?
- 为什么鹰能从高空发现地面的小猎物
- 为什么麻雀只会跳着走?
- 为什么黄土高原千沟万壑
- 为什么黄土高原有厚厚的黄土?
- 为什么黄土高原的黄土可以反映古气候
- 为什么黄山会形成"四绝〃?
- 为什么黄山多奇峰怪石
- 为什么黄山松都千奇百怪?