在牛顿和莱布尼茨发明微积分之前，数学家主要利用阿基米德的几何方法（即割圆术）来计算圆周率π。但是，要用割圆术求出较高精度的π值，需要计算很多边数的正多边形的边长或面积，这不是一件容易的事，鲁道夫·范·科伊伦花费了大半生的时间才将π算到小数点后35位。要求出更高精度的π值，单用几何方法已经是力所不能及了。
17世纪微积分的发明，使圆周率的计算进入了采用分析方法的时代。基于微积分和幂级数展开理论，人们发现了一系列用无穷级数表示的π的计算公式，这些公式不依赖于割圆术。第一个例子由苏格兰人格里高利于1671年得到，他利用arctanx的积分表示，得到了无穷级数展开式
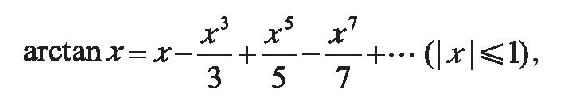
令x=1，就得到
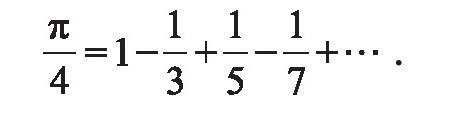
上式右端称为莱布尼茨级数，它不含根号，具有十分简单的形式，但其收敛速度很慢，还不适用于实际计算π，即使算300多项也算不出小数点后2位的准确数字。
1706年，数学家梅钦巧妙地改造了格里高利的公式，得到
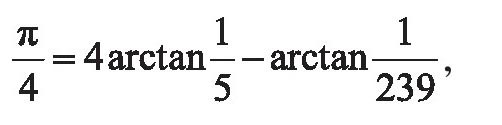
将格里高利级数代入，就得到收敛速度很快的级数表达式，这是π的第一个快速算法。梅钦本人用此方法计算π值到小数点后100位。以后，又陆续出现了计算速度更快的类似公式，统称为梅钦类公式。
伟大的数学家欧拉也为我们留下了许多有关π的重要公式，例如他证明了下面这些公式：
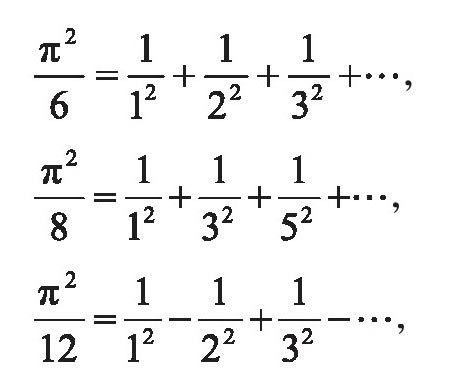
等等。
历史上，留下了各种各样含有π的计算公式，可以说数不胜数，所有这些公式的推导都离不开微积分。因此，微积分的创立极大丰富了计算π的方法。直到今天用电子计算机计算π的时代，其算法仍然是基于微积分推导出来的。例如，2002年算至1万亿位小数的算法，就是基于如下梅钦类公式：
可见，微积分的发明开创了圆周率计算的新纪元。（李大潜 善平）
巴黎发现宫π大厅墙壁上记录的π值
【微博士】布丰与投针实验
投针实验求圆周率
1777年的一天，法国数学家布丰在一张纸上画了很多条距离相等的平行直线，将许多等长的小针随意地投在纸上，小针的长度恰好等于相邻平行线距离的一半。布丰一共投了2212次，结果与平行直线相交的共有704根。总数与相交数的比值为3.142。布丰证明（这里需要用一点定积分知识），投的次数越多，这个比值就越接近π。后来，有许多人步布丰的后尘，用同样的方法计算π值。1901年，一位意大利数学家进行了多次投针试验后，得到了π的值约为3.1415929，与π的精确值相比，直到小数点后七位才出现不同。
【微问题】你能证明梅钦类公式吗？
【关键词】圆周率 阿基米德算法 刘徽割圆术 梅钦类公式
- 贵羊羊是谁?
- 贵重金属是什么？
- 贵金属有哪几种元素？
- 费城实验的经过是怎样的?当时的人穿越时空了吗
- 贾斯珀·琼斯为什么画美国国旗？
- 赖氏龙亚科与鸭嘴龙亚科有何不同？
- 赤丹茶花的病虫如何防治呢
- 赤潮是什么？它的成因又是什么？
- 赤潮是怎样形成的?
- 赤道附近为什么有雪山
- 走进北极近距离游览全球农作物种子库
- 赵州桥为什么那么有名?
- 赶走暑湿这些药材用起来
- 起身过猛时人为什么会感到眼前发黑?
- 超光速现象
- 超导性有哪些实际应用？
- 超巨星和红巨星怎么区别
- 超巨星的特点是什么
- 超强“烧烤"天气下该如何保护自己
- 超新星会毁灭地球吗
- 超新星爆发是什么？
- 超级大陆盘古最初因何而成？
- 超细纤维是什么时候发明的？
- 超速行车的危害有哪些?
- 超铀元素是什么？102—112号元素又都有哪些呢？