假如你有一个背包，最多能装30千克的东西。你有10样东西想装进背包里，它们的质量分别是13千克、1千克、9千克、4千克、5千克、27千克、8千克、8千克、14千克、17千克。显然，背包里装不下所有的东西。不过，你能试着把其中一半的东西装进背包里吗？
要想回答这个问题，最笨的方法当然是把所有可能的情况全试一遍。但是，要想从10件物品中任选出5件，一共有252（
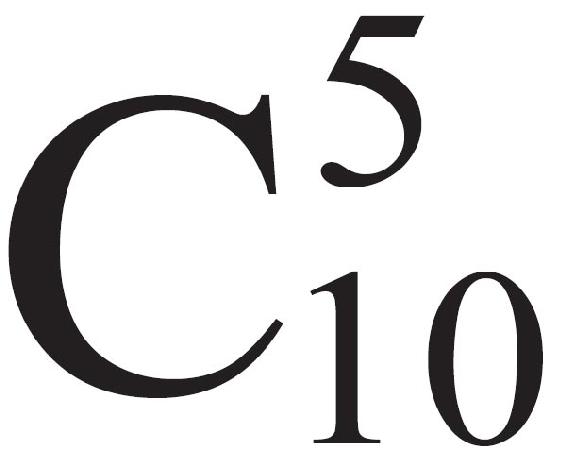）种方案，一个一个试起来就太慢了。其实，我们还有更聪明的方法，只需要检查一下，看背包里能否装下最轻的5件物品。如果连最轻的5件物品都装不下，其他情况就不用再试了。由于1+4+5+8+8=26＜30，因此我们的背包可以装下一半的东西。倘若背包的最大载重和物品的重量值都是上万上亿的数，并且等着装进“背包”里的物品也有成千上万件的话，那么即使用这种“聪明”的方法，也需要耗费大量的时间。好在，现在可以把任务交给计算机来完成。我们可以编写一个程序，把计算的方法（也就是所谓的“算法”）告诉计算机：首先，从左至右依次查看每一个数，不断把已经看过的数中最小的那一个和下一个数进行比较，这样就能选出所有数中最小的数。然后，把这个最小的数从这列数里面“拿”出来。如果有n件物品的话（不妨假设n是偶数），上述过程需要n-1次比较操作，以及1次把最小的数拿出来这个移动操作，总共n次操作。重新扫描剩下的数，再取出剩下的数中最小的数，拿出来，如此反复直到取出一半的数为止。这又分别需要n-1，n-2，…，（n/2）+1次操作。接下来，将取出的数加在一起，然后比较总和是否小于背包的载重。这需要（n/2）-1次加法运算以及1次比较操作。
因此，为了回答“背包里能否装下一半的东西”这个问题，计算机一共需要执行
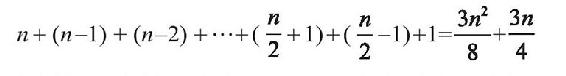
次操作。这是一个关于n的二次多项式。当然，在编写程序时，一些细节可能还需要很多额外的操作。不过，对于运算速度极快的计算机来说，这都可以忽略不计。现在的计算机每秒可以运算10亿次左右。即使n=1000，计算机也只需要0.0004秒就能得到答案。
如果一半数量的东西能顺利放进“背包”，我们接下来还要看看这样是不是充分利用了“背包”的最佳方案。刚才，我们把26千克的东西装进了背包里，但背包本来是可以装30千克的东西的，浪费了4千克不免有些可惜。于是，我们想到了另外一个问题：能否选择一些总质量恰好等于30千克的物品装进背包里呢？对于刚才的那组数据，我们只要试着组合几次就能得出结论，例如，13+1+8+8就恰好等于30。但若数据量太大，问题就只好又交给计算机来处理了。n个数的子集一共有2n个，换句话说，从n件物品中选出一些物品来（包括全选和不选）共有2n种方案。对于每一种方案，我们都需要最多n次运算来判断它是否满足要求，因此整个过程的运算次数需要大约2n×n次运算。随着n的增加，运算次数将呈几何级数上涨，其上涨速度与前面的多项式运算次数的增长完全不是一个级别！如果n=1000的话，运算次数将会是一个拥有300多位的天文数字，就算是超级计算机也需要昼夜不停地计算3.4×10287年。要说这个数字有多大？我们的宇宙最多也才1.38×1010岁！
多项式算法对计算机正常工作很重要
因此，为了让计算机正常运转，为我们解决更多的问题，所有实用、快速、高效的算法，其复杂程度都应该保证是多项式级别的；呈指数级增长的数量将会迅速失控，再强大的计算机也无法承受。因此，在为计算机编写程序解决实际问题时，我们往往希望有一个多项式算法。拥有多项式算法的问题就叫作P问题。（顾森）