月份牌上有国际通用的公历也有农历
中国目前使用的历法是国际通用的公历，也叫作阳历，它纯粹是由地球围绕太阳公转决定的。公历中有平年和闰年，平年一年365天，其中二月是28天；而闰年是366天，其中二月是29天。公历中的闰法是这样规定的：“四年一闰，百年少一闰，四百年加一闰。”为什么要这样规定呢？我们可以用“连分数”验证它的科学合理性。
已知地球绕太阳公转一周是365天5时48分46秒，而一个平年只有365天，因此必须把误差5时48分46秒，折算成天数，再通过加闰（二月的28天改成29天）的方法吸收这些积累误差。以天为单位，把这个误差写成分数形式是
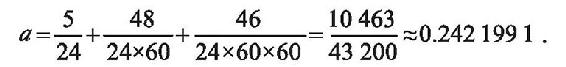
这表明43200年中应该有10463个闰年，想要消除误差，最好是均匀加闰，但这样既不便操作也不好记忆。用连分数近似可以提供便于记忆的闰法。
用辗转相除法不难得到误差a的连分数表示式为
由第一个渐近分数a1=1/4=0.25知道，每隔四年应该加一天，这就是“四年一闰”。当然，它是近似值，不够精确，还需要修正。由第三个渐近分数
知道，每隔33年加8天，即每隔99年加24天更接近于实际。这说明100年（近似于99年）应该加24天而不应该加25天，也就是说应该“百年少一闰”。
但是如果始终是每100年加24天，那么过了43200年，一共加了
432×24=10368（天）.
可是由a=10463/43200知道，过了43200年应该加10463天，少加了95天。这可不行！于是又进一步修正为“四百年加一闰”。
然而，按这种规定，可以算出在43200年中，一共加了10463天，又多加了13天，平均每3323年多加了一天。这就需要在历法中进行修正了。
由此可见，一方面，现行的历法是相当精确的，另一方面，还需要随时修正，而这一切都离不开数学。（徐诚浩）
【微博士】连分数
连分数是一种用特殊形式表示的分数。例如，考虑分数a=31/219。用辗转相除法可得如下分式：
把这两个分式合并可以得到一个连分数形式
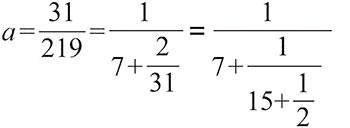
为了节省篇幅，我们把上述连分数缩写成
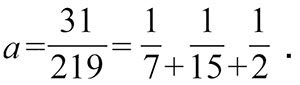
这里我们把加号写在下面而不是中间，表示加号后面的分数是加在分母上的。
连分数的好处是：对于一个复杂的分数a，可以通过其连分数的各个截断值，快速地求出用较简单分数表示的a的满意的近似值。
例如，a=31/219≈0.14155的逐个近似值为
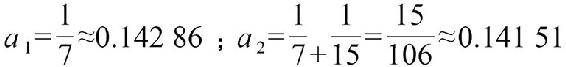
发现有关系式a2＜a＜a1。
无理数也有连分数表示法，只不过像小数表示一样，是一个无穷连分数。连分数的研究内容丰富，并有广泛的实际应用。
- “世界火炉"指的是哪里?
- “世纪彗星"浴火未重生奇迹之旅或已走到终点
- “两栖动物”一词是什么意思？
- “中国画"是什么样的画?
- “人兽"胚胎引发恐慌
- “仙鹤"为何是丹顶鹤
- “以糖治糖":治糖尿病还可以这么治
- “伽利略号”航天器的任务是什么？
- “低碳生活”怎么过
- “倾盆大雨”有多大
- “偷针眼"是怎样引起的
- “傻瓜"照相机是如何拍照的
- “像蝙蝠一样瞎”这一说法有何依据？
- “儿童专用"食品多半是忽悠
- “光污染”是如何造成的
- “六指”一定会遗传给下一代吗
- “冬眠"能使人延年益寿吗
- “剪刀石头布"的历史起源?
- “北斗":“在人群中总能精准看你一眼"
- “南艺"校花张蕊:中国首位航母女舰员
- “叉腰肌"是什么意思?
- “发育期疼痛”是什么造成的？
- “可燃冰”是理想的新能源吗
- “可燃冰”能帮我们封存大气中的二氧化碳吗
- “吃不逢时",再少也枉然