正所谓“无规矩不成方圆”，无论在古代中国还是在古希腊，圆规和直尺都是非常重要的作图工具。仅仅使用圆规和直尺的作图方法，就叫尺规作图。在它们的帮助下，古希腊人在几何学上取得了辉煌的成就。
正在绘制几何图形的古希腊数学家
古希腊人对圆规和直尺的使用方法有着严格的限制。圆规只能以某一点为圆心、某段长度为半径画圆，而直尺只能用来画出通过两点的直线，其上不标以刻度。这样的限制不仅体现了尺规作图的简单性，也使得古希腊人能用演绎推理的方法来证明作图的正确性。演绎推理可以说是现代数学研究方法的源头，而欧几里得的《几何原本》正是这种演绎推理的代表作。
但尺规作图并不是万能的。积累了丰富几何知识的古希腊人发现，对于一些问题，尺规作图似乎无能为力。其中最有名的三个问题被称为“古希腊三大几何问题”，它们是三等分角、倍立方和化圆为方问题。作出一个任意角的三等分线，这就是三等分角问题；给定一个任意的立方体，作出体积是它两倍的立方体的棱长，这就是倍立方问题；任意给定一个圆，作出面积与它相等的一个正方形，这就是化圆为方问题。
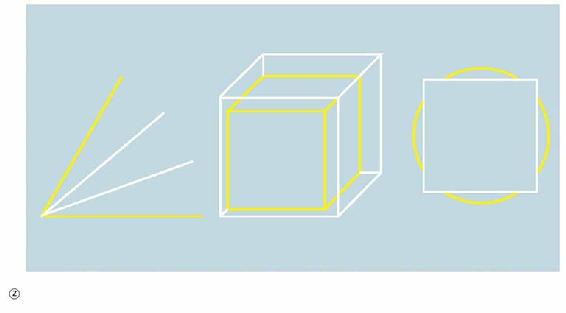
古希腊三大几何问题
从古希腊到现在，不断有人研究这三个问题，希望找到尺规作图的解法。但在长时间的努力后，人们开始怀疑，尺规作图是否能解决这三个问题？更进一步地说，尺规作图能解决什么问题？
解析几何的出现，给了数学家研究几何问题的新方法。通过坐标的计算，我们可以将几何问题转化为代数问题。因为直线和圆相当于一次方程和二次方程，尺规作图在代数上相当于一个二次方程组。而通过对于代数方程和抽象代数的研究，数学家发现，从单位长度出发，尺规作图可以作出的长度，恰好是自然数通过有限次四则运算和开平方能得到的所有数。
至此，数学家终于能解答古希腊三大几何问题了。
对于三等分角问题，我们可以假设尺规作图时给定了一个单位长度，那么，作出一个角相当于作出这个角的正弦值。我们能作出60°的角，因为60°的正弦值是
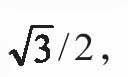可以通过有限次四则运算和开平方得到；但它的三分之一，也就是20°的角，其正弦值不能通过有限次四则运算和开平方得到。所以，尺规作图三等分60°是不可能的，三等分任意角就更不可能了。对于倍立方问题，如果将给定立方体的棱长看作单位长度，倍立方问题相当于作出
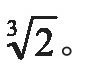虽然看起来简单，但这个数不能通过四则运算和开平方得到。所以，尺规作图是不能解决倍立方问题的。对于化圆为方问题，如果将给定圆的半径看作单位长度，化圆为方问题相当于作出
但在1882年，德国数学家林德曼证明了π是一个超越数，不仅不能通过有限次四则运算和开平方得到，更不是任何整系数代数方程的解。所以，尺规作图同样不能解决化圆为方问题。在数学中，这种借助另一分支来解决问题的情况经常发生。古希腊三大几何问题属于几何的范畴，但它的解答要借助代数的力量。哥德巴赫猜想属于数论的范畴，但陈景润在哥德巴赫猜想方面的工作用到了大量的数学分析。虽然数学拥有众多的分支，每个分支看似互不相干，但实际上它们之间有着千丝万缕的联系。在一个领域内的难题，有时可以用另一个领域的方法解决。这些出人意料的联系，正是数学的活力和魅力所在。（方弦）
- 是否有会飞的恐龙？
- 是否有关于较为近期小行星杀手的证据？
- 是否有其他动物捕食恐龙？
- 是否有多次获得诺贝尔奖的得主？
- 是否有恐龙在白垩纪大灭绝中幸存？
- 是否有恐龙生活在寒冷的极地地区？
- 是否有恐龙皮肤的化石？
- 是否有恐龙蛋白承受住数百万年的埋藏而幸存？
- 是否有科学家认为印石版始祖鸟是恐龙和现代鸟类的过渡？
- 是否有让人在生活中更加成功的“智力”
- 是谁发明了世界上第一台计算机
- 是谁吃掉了墨西哥湾的石油
- 是谁在开火星车
- 是谁最早发现了浮力定律？
- 是谁最早提出恐龙是温血动物的？
- 是谁破译了元素的“密码”
- 是谁证明物质是由分子组成的
- 显微镜都有哪些共同元件？
- 晒干的洋葱为什么会发芽?
- 晚上为什么能从窗外看清屋里的东西?
- 晚餐为什么不宜吃虾皮
- 晚饭为什么不要吃得太饱?
- 晚香玉为什么夜里才来香
- 普米族的有哪些礼仪和禁忌风俗习惯介绍
- 普通人体内有多少DNA？