市场上水果店老板堆水果的方法对空间利用率最高
“水立方”是现代建筑的杰作，也是科技与艺术结合的典范，可是你知道吗，水立方涉及一个著名的数学猜想——开尔文问题。
1887年，受比利时物理学家普拉托泡沫研究的启发，当时正在思考以太问题的英国著名物理学家开尔文勋爵提出了著名的“开尔文问题”：如果将三维空间划分为一个个给定相同体积的空腔，为保证它们的接触面积，也就是表面积最小，这些空腔应该是什么形状？
开尔文给出的答案是“截角八面体”，就是将正八面体的6个角截去，所得到的一个十四面体。开尔文猜想，单位体积的截角八面体具有能填充空间且表面积最小的性质。100多年来，这个猜想始终未得到证实或否定。同样的问题放在二维平面上，就是我们都很熟悉的蜂房：每一个蜂室都呈六角形，这样最节省蜂蜡，这也是大自然在漫长进化中做出的最优选择。不过，即使是这个看上去显得颇为直观的“蜂巢猜想”，也折腾了数学家不知多少年，有人认为这一问题甚至可追溯到古希腊数学家帕普斯。“蜂巢猜想”直到1999年才被美国数学家黑尔斯解决：如果把平面划分成无数块，每块都具有相同的给定面积，则这些块的周长达到最小只有一种可能，即每块都是正六边形。
三维空间无疑复杂得多。1993年，爱尔兰的两位物理学教授威尔和弗兰受到一种称为笼结构的化合物的启发，终于得到了超越开尔文的方案。1994年，他们发表了这一结果：采用十四面体（与开尔文的十四面体不同）与十二面体（不是正多面体）的组合，其接触表面积比开尔文结构要减少3%左右。不过，人们至今也不知威尔和弗兰的方案是不是就是最佳方案，不过这个方案能够超越开尔文方案已经相当不错了。
2003年，澳大利亚ARUP公司的工程师卡夫雷偶尔看到办公室里挂着的几幅几何图形，大受启发，并因此绘制了用于2008年北京奥运会的、极具个性的“水立方”设计雏形。建成后的“水立方”采用的正是威尔-弗兰模型，75%的十四面体和25%的十二面体的组合，为保证整个外观仍是长方体，大约100个“多面体”被切断。整个建筑仅用6700多吨钢，建筑空间能够容纳上万名观众。它外立面中的多面体在夜幕中散发着晶莹的蓝光，是一座数学与建筑完美结合造就的奇迹。（田廷彦）
【微博士】开普勒猜想
1611年，德国著名科学家开普勒提出：在一个大的容器里，相同大小的硬球如何排放，才能放得尽可能多？开普勒找不到比市场上水果店老板堆放水果的方式更好的方法了。他猜想这就是最佳方法。开普勒猜想说，这是所有可能的装球排列法所能达到的最高密度，没有更高的了。1998年，美国密歇根大学教授黑尔斯利用强大的计算机技术，宣布解决了开普勒猜想，答案是肯定的。但是黑尔斯的证明还有待考证。
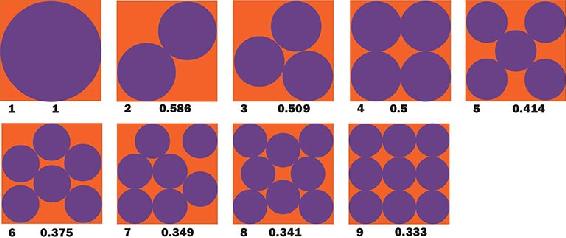
【微问题】如果要包装5个乒乓球，怎样包最节省包装材料？
【关键词】生物几何 开尔文问题