科赫曲线看上去有头有尾，除了弯弯曲曲外似乎没有什么特别的，但它却有无限的长度，真是非常奇特。
科赫曲线还有其他奇特之处，比如，三条科赫曲线首尾相接可以围成一个雪花形的图形，称为科赫雪花曲线，它围成的面积是有限的，但它的周长却是无限的。科赫曲线处处不光滑，其上任何一点处都没有切线。科赫曲线上任取一小段，都可以无限拉长，但无法拉成一条直线，怎么拉都是弯曲的。
圆周
科赫雪花曲线
那么为什么圆周可以求出其长度，而同样围成有限面积的科赫雪花曲线却不可求长呢？比较一下圆周和科赫雪花曲线，立即可以发现它们本质上的区别：圆周是光滑的，而科赫曲线处处不光滑！何为光滑呢？在数学上就是说它处处有切线，在切点附近，曲线和直线（切线）非常接近。为此，我们将通过光滑曲线的局部放大来观察曲线的局部形状。
如果把圆周上一点进行局部放大，从中可以明显地看出圆周上一点附近很小的局部和直线非常接近。
这样，在测量时，用小而直的尺代替这一小段曲线几乎没有什么损失，测量得到的误差微乎其微，并且随着尺长的缩短，总的测量误差会越来越小，最后达到曲线的实际长度。
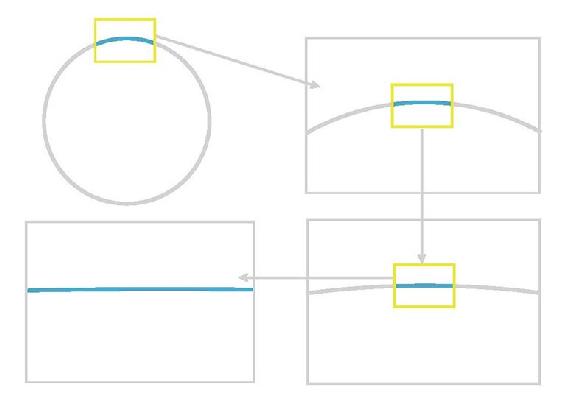
圆周局部放大图，圆周上的一小段和直线段相差无几
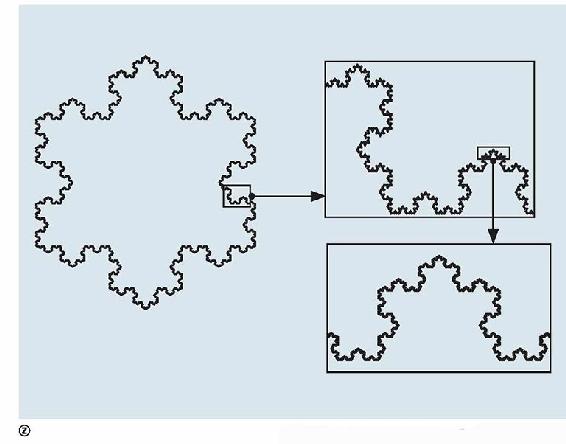
科赫雪花曲线任何一小段都和原曲线同样复杂
反观科赫雪花曲线，任何一小段经过放大，可以发现其与整条曲线是相似的，包含了原来整条曲线的复制品。这样，任一小段都和原曲线同样复杂，永远不会变得和直线近似。因此，科赫曲线上再小的一段都不能用直尺来近似地替代，自然不能用直尺来测量出科赫曲线的长度。科赫曲线这种任意小局部都和整体相似，且和整体一样复杂的性质，称为自相似性。具有自相似性质的几何对象现在有一个新名字——分形。第一条具有这种点点不光滑、处处没有切线、不可求长等性质的曲线，是由德国大数学家魏尔斯特拉斯构造的，称为魏尔斯特拉斯曲线。在魏尔斯特拉斯构造出他的曲线之前，大多数人认为一条曲线除少数点外，其他地方都应该是光滑的、有切线的，曲线段都是有确定长度的。而魏尔斯特拉斯曲线的出现打破了人们的固有观念，堪称一大创举。不过魏尔斯特拉斯曲线比较复杂，而科赫曲线的构造比较有规律，容易被大家接受，是介绍不可求长曲线的好例子。
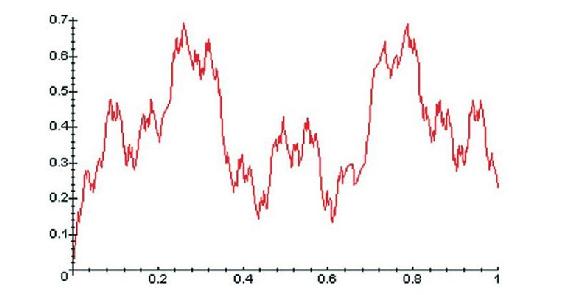
魏尔斯特拉斯曲线
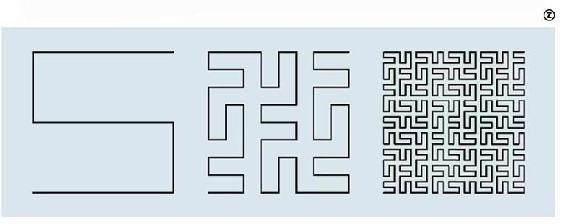
皮亚诺曲线
事实上还有更奇特的曲线存在，比如，意大利数学家皮亚诺构造了一条曲线，称为皮亚诺曲线，这条曲线居然可以充满整个正方形！当然，这条曲线也绝对是不可求长的。（邱维元）
【微问题】想一想，海岸线长度能精确测量吗？
【关键词】曲线长度 不可求长曲线
- 为什么坦克底部要开一扇门
- 为什么坦克曾被誉为“陆战之王”
- 为什么坦克炮塔的装甲特别厚?
- 为什么坦克的生存力很强
- 为什么坦克能在原地“掉头"?
- 为什么坦克能在荒野上疾驰如飞
- 为什么坦克要安装履带?
- 为什么垃圾不能“一埋了之"
- 为什么垃圾不能“一埋了之”
- 为什么垃圾食品特别诱人
- 为什么埃及的雕刻人像看上去特别僵硬？
- 为什么埃塞俄比亚被称为"咖啡的故乡"?
- 为什么埃尔·格列柯的绘画看上去很现代？
- 为什么城市中的公交车多种多样
- 为什么城市会爆发“垃圾危机”
- 为什么城市垃圾要作分类处理
- 为什么城市易被洪水围困
- 为什么城市的天空经常灰蒙蒙的
- 为什么城市越来越大而不是越来越小
- 为什么城市里会堵车
- 为什么城市里的植物“不喜欢”雪
- 为什么城市里的植物“不喜欢"雪
- 为什么城市里的燕子越来越少了
- 为什么城市高架铁路是安全的?
- 为什么基因发挥作用离不开环境因素