ii竟然是实数！这件事很让人感到意外，也很有趣。现在，我们来解释其中的原因。这涉及复数的复数次幂的定义。一切可以从著名的欧拉公式eiθ=cosθ+isinθ出发。利用三角公式，复指数eiθ有我们通常实指数一样的性质，比如
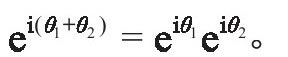这样，对一般的复数z=x+iy（x,y为实数），就有复指数ez=ex+iy=exeiy=ex(cosy+isiny).
对于z=x+iy≠0，记
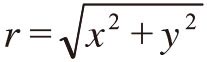，可以将x，y写为x=rcosθ，y=rsinθ，（-π＜θ≤π）.
这样，复数z又可表示为
z=r（cosθ+isinθ）=reiθ，
称为复数z的指数表示。由于三角函数是周期为2π的周期函数，可以看出复数z的指数表示不唯一。事实上，对任意整数k,z=rei（θ+2kπ）。
我们知道，对数是指数的逆运算，这对复指数也应成立。这样我们可以有复数的对数：如果z=rei（θ+2kπ），那么
lnz=lnr+lnei（θ+2kπ）=lnr+i（θ+2kπ），k=0，±1，±2，…
这里出现了一个奇怪的现象：复数的对数居然有无穷多个值。而k=0时，即lnz=lnr+iθ称为对数lnz的主值。
现在我们可以利用复指数和复对数来定义复数的幂zα了。如果α=n是自然数，zn就是n个z相乘。当α是一般的复数时怎么办呢？我们依靠指数函数与对数函数来定义：
zα=eαlnz.
这样定义的合理性在于：对于正实数x,a＞0，我们已经有xa=elnxa=ealnx。很显然，对一般的复数α，zα也有无穷多个值。
现在我们来看看ii究竟该等于多少？由于i=cos（π/2）+isin（π/2）=eiπ/2，按定义，有
于是，
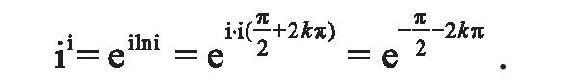
可见，ii的确是实数，其主值等于e-π/2。（李忠）
【微问题】你还能举出欧拉公式的其他应用吗？
【关键词】欧拉公式 复指数