到底等于多少到底等于多少讨论这个问题之前，我们需要对调和级数有个简单了解。
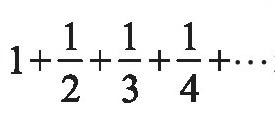称为调和级数，这个级数中的通项是
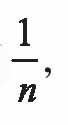显然，随着n的无限增大，
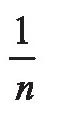会无限制地减小。调和级数究竟是无限大，还是等于一个固定的正数呢？这并非一个一目了然的问题。14世纪法国学者奥雷姆巧妙地证明了
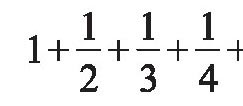…是无穷大。到了17世纪，瑞士数学家约翰·伯努利给出了一个新的证明，此证明就发表在其兄雅各布·伯努利的著作中。接着，他们进一步说明
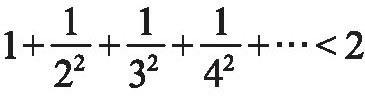，但却无力求出
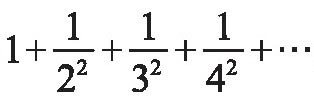的确切值。雅各布·伯努利不无遗憾地说：“如果有人能够发现并告知我们迄今为止这一尚未解决的难题的答案，我们将不胜感谢。”
后来，解决这个问题的人终于出现了，他正是18世纪最伟大的数学家欧拉。
为了求得这一值，欧拉先后对此式计算到小数点后第七位及第十二位，但这算的是近似值，1735年，欧拉考察了一个与正弦有关的函数并将其展开形式结合“韦达定理”，最终求得
。
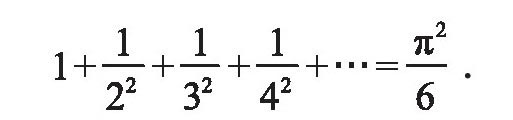由于这项成就，欧拉一下子出了名。其实，这个问题最早是1644年意大利数学家门戈利提出的。现在这个问题被称为“巴塞尔问题”，巴塞尔是伯努利家族和欧拉的故乡。欧拉的证明方法不太严格，不久以后，严格的证明找到了，特别是利用傅里叶级数理论可以很容易地进行证明。
利用极限的观点（可以先计算不大于某个自然数k的任两个自然数互素的概率，然后令k趋向于无穷），很容易证明，任意两个自然数互素的概率为
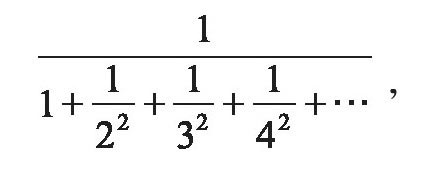
于是由上述欧拉证明的结果，我们知道它就是
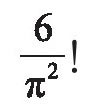（田廷彦）【微博士】巴塞尔问题
巴塞尔问题是一个著名的数学问题。这个问题是以瑞士第三大城市——巴塞尔命名的，它是欧拉和伯努利家族的家乡。这个问题是精确计算所有平方数的倒数的和，也就是以下级数的和：
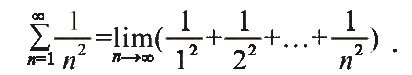
这个级数的和约等于1.644934。巴塞尔问题是寻找这个数的准确值，并证明它是正确的。1644年，皮耶特罗·门戈利提出了这一问题，欧拉发现准确值是
并在1735年公布。
- 景颇族有什么礼仪和禁忌习俗介绍
- 晴天的夜里为什么很冷?
- 晴朗的天空为什么是蓝色的?
- 智人“走出非洲”的历程在世界各地都一样吗
- 智力发育为什么要依靠营养合理?
- 智能机器人究竟是好还是坏
- 晾在院子里的衣服为什么干得快?
- 暖心!流浪狗帮爷爷清理街道,狗狗:你若不离我便不弃!
- 暖色与冷色有什么区别？
- 暗物质是什么东西?
- 暴雨会带来哪些危害
- 暴雨时如何保证驾车安全
- 暴雨期间应该遵守哪些安全规则？
- 暴饮暴食为什么会伤身
- 曳压型断裂
- 曳裂型断裂
- 更大的细胞是什么时候开始发展的？
- 曹操为什么至死不称帝?
- 曹操为什么要建72座陵寝?
- 曹操是一代枭雄还是大政治家?
- 曼陀罗的盆栽管理需要注意什么
- 曾经失踪的太阳中微子找到了吗
- 曾经的夏都:河南偃师二里头遗址
- 最亮的恒星有哪些？
- 最亮的星是什么星?