1883年，德国数学家康托尔向人们展示了这样一个非常怪异的集合。考虑由0到1之间的所有实数构成的区间[0，1]，把它平分成三段，并去掉中间那一段开区间（1/3，2/3）。这样，剩下的集合是两个剩余区间的并集，即[0，1/3]∪[2/3，1]。接下来，把每个区间都再次分成三段并挖掉中间那段开区间，于是便得到了由四个更小的剩余区间构成的集合
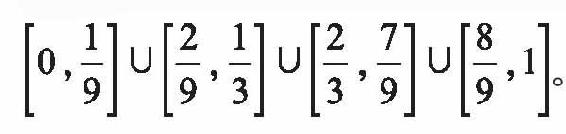继续在每个区间中挖掉中间三分之一，并无限地这样做下去，最后剩下的数所组成的集合就叫作康托尔集。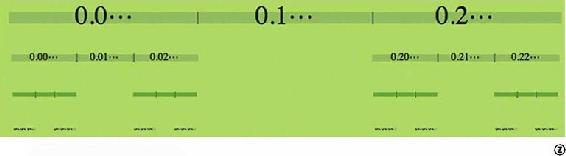
康托尔集的构造过程
容易看出，每次挖掉各个区间的中间那一段之后，所有剩余区间的总长度将会变为原来的2/3。由于初始时区间的总长度为1，第n次操作之后所有剩余区间的总长度便只剩下（2/3）n。当n趋于无穷大时，（2/3）n将趋于0，可见康托尔集的“总长度”为0。
不过，这只能表明康托尔集内不含有任何区间，并不能表明康托尔集里不存在任何数。在生成康托尔集的过程中，由于每次挖掉的是一个开区间，各个剩余区间的端点都不会被挖掉，因而像1/3，2/3，1/9，2/9，7/9，8/9之类的数最终都将保留在康托尔集里。事实上，由于所有形如（1/3）n的分数都会保留下来，因而康托尔集里的数有无穷多个！更有趣的是，康托尔集中还包含了很多“端点值”以外的数。如图所示，用线段AB表示区间[0，1]，A'B'表示区间
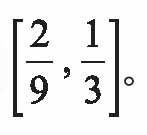如果点P满足AP∶AB=A'P∶A'B'的话，那么点P将始终以相同比例的位置留在越来越小的剩余区间中，永远也不会被挖掉。假设点P所代表的数是x，那么x应该满足
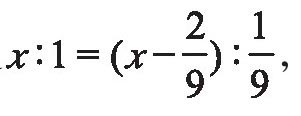可以解得x=1/4。它也是康托尔集里的数。
端点以外的点，也可能在康托尔集内
尽管康托尔集里的数有无穷多，但直观上似乎应该比[0，1]区间中的实数少得多。然而令人惊奇的是，这是不对的，实际上康托尔集里的数和[0，1]区间里的实数一样多！它比看上去布满[0，1]区间的有理数要多得多！
为了说明这一点，我们把0到1之间的所有数都用三进制小数来表示。如果把这些数平均分成三段，那么它们正好依次是0到0.1之间的数，0.1到0.2之间的数，以及0.2到1之间的数。挖掉的中间那一段的数正好是小数点后第一位是1的那些数，而剩下的数都是那些小数点后第一位是0或者2的数。在下一步中，我们将挖掉每个区间的中间1/3，也就是所有小数点后第二位是1的数，剩下的数便都是那些小数点后第二位也是0或者2的数……不断这样操作下去，最终留在康托尔集里的数，恰好就是那些只由0和2构成的三进制小数！比如1/4的三进制小数表达是0.020202…，可见1/4确实属于康托尔集。另外，虽然1/3的三进制小数是0.1，1/9的三进制小数是0.01，但我们也可以把它们分别改写成无限循环小数0.02222…和0.002222…（这个道理和0.999…=1是一样的），因此它们也在康托尔集里。
接下来，我们就能轻易地把康托尔集里的数与[0，1]区间里的所有实数一一对应起来。对于康托尔集里的任意一个数，首先把它转化为三进制小数，把小数展开中的所有数字2变成数字1，再把新的小数当成是二进制小数，并重新转化回十进制，它就是[0，1]之间的某个实数。同样地，对于[0，1]区间的每一个实数，先把它写成二进制小数，再把所有的1都改写成2，并把它看作是一个三进制小数，它便成了康托尔集里的一个数。因此，康托尔集里的数和整个[0，1]区间里的实数之间存在一一对应关系，两个集合里的数是一样多的！
康托尔集的“总长度”为0，但所含元素的个数竟然和实数区间一样多，这些奇异的性质迅速引起了数学家们的注意。在集合论、拓扑学、测度论、实分析、分形理论等各个数学分支中，康托尔集都扮演着重要的角色。（顾森）
【科学人】康托尔
康托尔（1845—1918），德国著名数学家，生于圣彼得堡。1856年举家搬到法兰克福。1867年，康托尔获得柏林大学博士学位。康托尔最杰出的贡献是集合论的创立。在康托尔之前，数学家大多将无穷大看成是一个虚幻的东西，它的存在仅仅是为了叙述问题的方便。康托尔则不然，他引入了“势”的概念，并且一个无穷集合的势可以比另一个无穷集合的势大。一个最著名的例子是，偶数与自然数、有理数一样“多”，但比无理数、实数“少”！这正是康托尔第一个证明的（1873年），并可看成是集合论诞生的标志。这无疑需要极为丰富的想象力和非凡的勇气。康托尔受到的打击也是非同寻常的，为此他找不到最好的大学任教，并患上抑郁症，最后死在精神病院里。
【微博士】连续统
（0，1）区间上的实数全体也称为“连续统”。所谓的“连续统假设”就是断言：不存在比全体自然数那种无穷更大，同时又比全体实数那种无穷更小的某种无穷。这是著名的“希尔伯特23个问题”当中的第一个。数学家已经证明，在现有数学体系中承认它或否定它都不会产生矛盾。
【微问题】你能在闭区间[0，1]和开区间（0，1）之间建立一一对应吗？
【关键词】无穷大 康托尔集