通过日历可以方便地查到某天是星期几
需要知道某一天是星期几，但是手头却没有万年历可查。解决的办法有很多，其中有一种是从《七色表》中查找。
《七色表》由五个栏目组成：“星期栏目”、“月份栏目”、“日期栏目”、“公元年份栏目”和由红、橙、黄、绿、青、蓝、紫七种颜色组成的“七色栏目”。
查找方法如下：先在“月份栏目”内找到所查月份所在的横行，在“日期栏目”内找到所查日期所在的竖列，并在它们的交会处确定并记住这个颜色；再在“公元年份栏目”内找到所查年份，在此行中往左查到所记住的颜色，再往上在“星期栏目”内即可找到所需的星期数。
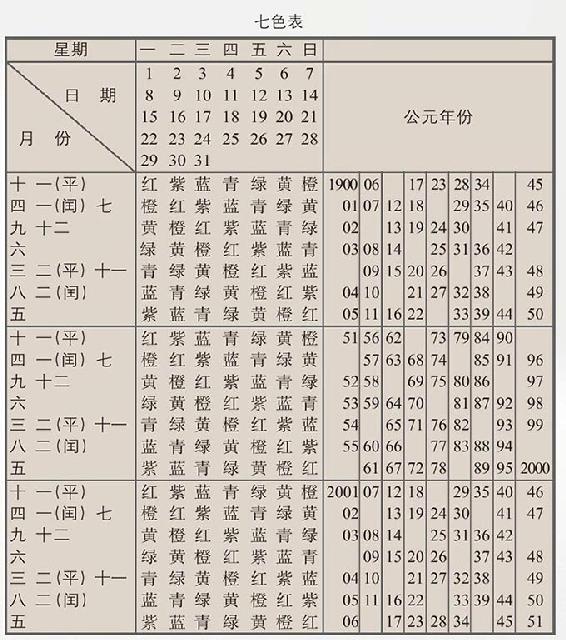
注：一（平）和一（闰）分别表示平年和闰年的一月。
二（平）和二（闰）分别表示平年和闰年的二月。
例如，如果要查1937年4月7日是星期几，先在“月份栏目”内查到四月，再在“日期栏目”内查到7日。在交会处查到黄色。再在“公元年份栏目”内查到1937年，往左找到黄色，再往上即可找到星期三。
这张《七色表》应用非常简单，但是似乎“玄不可测”，它是怎样编制出来的呢？
大家知道，如果已经知道某年的元旦（1月1日）是星期几，那么这一年中任意一天的星期数是不难算出来的，只要正确求出这一天与元旦之间相隔多少天就可以了。
把公元x年元旦的星期数称为该年的“年代号”，记为Nx，它的取值集合是{0，1，2，3，4，5，6}，其中0表示星期日。我们要找到一个能求出任意一年的年代号的公式。
假设公元1年的元旦是星期一，也就是它的年代号N1=1。如果根据这个假设推导出来的公式，所求出的每个年的年代号都是正确的，那么，这个假设当然是正确的了！
因为每个平年有52周加1天，每个闰年有52周加2天，所以有
N1=1，N2=2，N3=3，N4=4，N5=6，N6=0，N7=1，…
也就是说，如果x是平年，那么Nx+1=Nx+1；如果x是闰年，那么Nx+1=Nx+2。于是根据阳历“四年一闰，百年少一闰，四百年加一闰”的闰法立刻得到公式
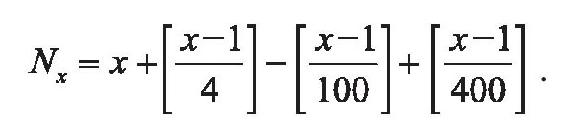
其中，中括号内的数值都表示其中分数的整数部分。这三个中括号的计算结果的数值就是在公元1年到x年之间一共出现的闰年个数。容易求出21世纪以下各年的年代号：
如果需要知道x年y月z日是星期几，那么，先求出年代号Nx。再求出从1月1日算起，到y月z日前一天的总天数h（不包括y月z日这一天），它就是在前y-1月中，大月的月数乘以31（或者乘以3），加上小月的月数乘以30（或者乘以2），再加上2月的28或者29天（或者加上0或1），再加上z-1。最后把S=Nx+h除以7，所得的余数就是所要求的星期数。
如果认为总天数h的计算太复杂，那么可以用“月代号法”。
因为如果知道某个月的1日是星期几，那么很容易求出这个月的任意一天是星期几，所以只要知道这一年中12个月的1日是星期几就可以了。这12个数字就构成了这一年的“月代号数列”，这种数列是可以根据阳历的大小月和闰法确定的，而且有明显的规律性，如下表所示，其中有12个粗体数字表示比上一年对应的同月数字多2，而其他的地方都是多1。
根据这种“月代号数列”就制造出了《七色表》。
必须提请注意的是，从公元前45年起，到1582年10月4日，用的是儒略历。现在通用的格里历，从1582年10月15日开始，中间有10天是跳过去的。所以，所有查找星期的方法都只适用于格里历。（徐诚浩）
【微博士】儒略历与格里历
从公元前45年起，罗马人开始采用罗马皇帝儒略·恺撒（前102年—前44年）制定的儒略历。此历法规定一年中有七个月是31天，四个月是30天，2月为28天。每隔四年，设一闰年（2月为29天）。
在这样的历法规定下一年共有365.25天，比365.2422天（即地球绕太阳转一圈是365天5小时48分46秒）多了11分14秒。到了1582年，由于误差逐年积累，春分由3月21日提早到了3月11日，于是，在1582年10月4日罗马教皇格列高利十三世命令10月5日改为10月15日（中间10天是没有的），并且颁布格里历，它就是现在通用的公历。
【微问题】假如只告诉你元旦那天是星期几，你能找到一个用来求星期数的公式吗？
【关键词】求星期数 儒略历 格里历
- 为什么南极会被污染
- 为什么南极冰盖会“走路"
- 为什么南极冰盖会“走路”
- 为什么南极比北极冷?
- 为什么南极洲的陨石特别多
- 为什么南极的一些动物会失明
- 为什么南极的陨石特别多?
- 为什么南非被称为“黄金之乡"?
- 为什么卫星看地球更有优势
- 为什么卫星能观察到地面的情况
- 为什么卫生间不能对着卧室?
- 为什么印加人信奉太阳神?
- 江苏靖江有什么名胜古迹
- 江西人为什么被称作“老表"?
- 江西萍乡名胜古迹有哪些
- 池塘里的冰块曾被用来当作首台冷凝装置吗？
- 池水为什么是绿色的?
- 污染物有哪几类?
- 汤达鸠远征中挖掘出了什么恐龙遗骸？
- 汽水是怎么做出来的?为什么会冒那么多泡泡呢?
- 汽油、燃油、石油的区别是什么
- 汽油中的铅是哪里来的
- 汽油中都有哪些添加剂？它们都有什么作用？
- 汽油替代燃料作为机动车动力的优缺点有哪些？
- 汽油的辛烷值是什么？