由三角形的内角和都是180°或π，很容易知道，平面上一般n边形的内角和等于（n-2）π。这一点，只需要将多边形从一个顶点出发依次将其切分为n-2个三角形即可证明。这个结论依赖于边数n。一个更一般且更本质的结果是：任何凸n边形（每个内角都小于180°的多边形）的外角和都是360°。这是一个不依赖于边数n的不变量，体现了数学的常数美和统一性。其证明也非常简单。任何一个凸n边形都有n个内角、n个外角，每一个内角及其相关外角之和正好等于1个平角。所以，凸n边形所有n个内角、n个外角之和为n个平角nπ，又已知n个内角之和为（n-2）π，因此n个外角之和必为2π。需要注意的是：对于凹的多边形，要使结论仍成立，某些外角必须被定义成负的。
为什么说n边形的外角和等于2π是一个更本质的结果呢？我们换一个角度对此做一个解释。让一条直线贴着多边形的边逆时针转动，遇到角时就从一边转这个角到另一边，这样，该直线转过的角度就是这个角的外角。如果让这条直线绕多边形的边转一周，再回到起始位置，则该直线所转过的角度，就是多边形的外角和2π。现在让圆周的切线绕该圆周转一周，回到起始位置，立即可以发现，该切线所转过的角度也是2π。这并非巧合，事实上，在平面上任意画一条分段光滑不自交的闭曲线，这条曲线的切线绕曲线一周（遇到顶角就转过顶角），其改变的角度同样也是2π。这显示了这种曲线的内在性质，凸多边形只是其中的一个特例而已。
曲线的切线在一点附近移动单位长度，其所改变的角度大小，描述了曲线在该点附近的弯曲程度：角度越大，曲线越弯曲，反之则较平坦。曲线在这一点处的弯曲程度，称为曲线在该点的曲率。上面的结论说明分段光滑不自交闭曲线各点处的曲率之“和”，再加上转角处的外角和，等于2π。当然由于曲线上的点多到无法数清，这里的曲率之和不再是通常意义上的求和，要用微积分理论里的积分来表示。对曲面上的曲线，也有类似的结论。由于曲面也是弯曲的，曲面也有曲率，我们不但要考虑曲线的曲率，还要考虑曲面的曲率，这就是微分几何里著名的高斯-博内定理。值得一提的是，著名的华人数学家陈省身先生证明了高维的高斯-博内定理，构造了现今普遍使用的“陈示性类”，为现代整体微分几何奠定了基础，成为一代微分几何大师。（张文俊）
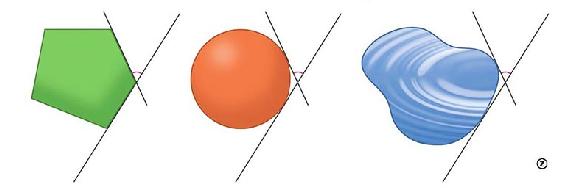
外角角度等于直线从一边绕角转到另一边的角度，在曲线上相当于切线转过的角度
【微问题】你能否给出欧拉公式的严格证明？
【关键词】正多面体 欧拉公式
- 乳糜泻患者适合什么饮食？
- 乳香和没药是从哪里来的？
- 乳香和没药来自哪里？
- 乳齿象和猛犸象有什么不同？
- 乳齿象是如何灭绝的
- 了解弱视别对视力问题抱有侥幸心理
- 二代步兵战车
- 二十六亿年的液态水
- 二哈到超市搞突击检查,结果吧收银员吓一大跳。
- 二哈和主人吵架,吵输了居然这样,主人看了瞬间笑抽了
- 二哈在家天大地大它最大,结果主人带它来医院,瞬间怂成这副样
- 二哈妈妈为了不让孩子喝奶,居然想出了这么一个主意...
- 二哈妈妈嫌带孩子太累,把宝宝都叼到了邻居家让其照顾
- 二哈想要拆家,猫咪直接教它做狗
- 二哈爱拆家,主人想了一个办法
- 二哈老叫,让后猫咪发飙了一顿胖揍,主人:事实证明这只二哈是纯血的
- 二哈转行做保姆,甘愿为宝宝当枕头,网友:二哈这画风不对呀
- 二战中德国进攻苏联的原因
- 二战中法国投降仪式为什么在车厢举行
- 二战前的中德关系如何
- 二战日本战败的原因是什么
- 二战的历史背景是什么
- 二手烟有害吗？
- 二月兰的种植方法是怎样的
- 二氧化碳意外使地球变更绿