自从引入虚数单位i=
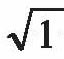后，数学家在解决数学问题时开始越来越多地使用复数。尽管如此，数学家最初却并不承认复数是真实的数，认为它是虚无缥缈的东西，是想象出来的数。大数学家欧拉对复数的研究有重大贡献，虚数的名称以及虚数单位符号i就是由欧拉引进的，他还给出了著名的欧拉公式eiθ=cosθ+isinθ.
可是欧拉同样不承认复数的真实性。他说：“一切形如
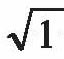与
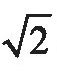的数，都是不可能的，因为所表示的是负数的平方根。对于这一类数，我们只能断言，它们既不是什么都不是，也不比什么都不是多些什么，更不比什么都不是少些什么。它们纯属虚构。”这种局面一直持续了近200年，直到19世纪高斯的时代才得以结束。我们知道，实数都可以用数轴上的一个点来表示，那么，该如何表示虚数i呢？当时，欧洲的几位数学家威瑟尔、阿尔冈和高斯等人注意到，一个数乘以-1等于它的相反数，在数轴上就是绕原点O转了180°，如果再乘以-1则相当于再转180°回到原来的位置。现在i2=-1，这表明一个数连乘两次i就相当于绕原点转180°，这样，乘一次i就应该是（逆时针）转了90°。由此可以想象，所有纯虚数都应该在一条过原点且垂直于实数轴的直线上，这就是虚轴。将原来的实数轴称为实轴，实轴和虚轴就构成了一个平面直角坐标系，而复数a+bi就代表此直角坐标平面上的一个点（a,b）。用复数表示的平面称为复平面。
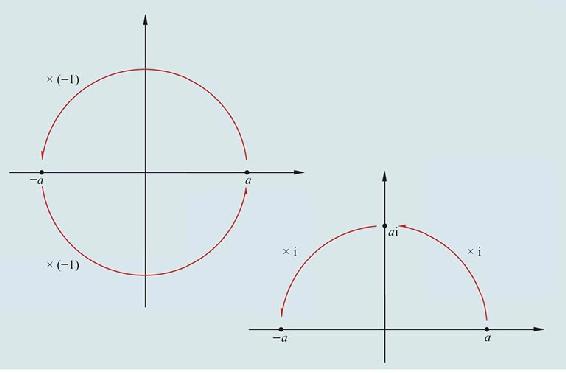
虚轴的构造产生了复平面
这种方法使得，复数及其加减乘除运算都有了明显的几何意义。从此，复数有了一个实际的模型，人们对它也便有了真实感。原本虚无缥缈的复数，变成了实实在在的东西。
高斯等人的这一模型，不仅为复数带来真实感，消除了人们的疑惑，而且把复数与平面几何、向量运算联系在一起，使得许多平面上的数学、物理问题得以应用复数的工具。
到了19世纪，在此基础上发展起来一门学科——复变函数论，是微积分在复变量函数上的延拓。复变函数在流体力学与弹性力学中都有重要应用，比如机翼的设计会用到复变函数中的共形映射。更令人意外的是，复变函数还被用来研究素数分布，并且发展成现代数学的一个重要分支——解析数论。在当代数学中，无论是纯数学，还是应用数学，都离不开复数。
过去的人无论如何也没有想到，这种“纯属虚构”的数，如今竟是如此神通广大。（李忠）
【微博士】四元数
复数a+bi代表直角坐标系上的一个点（a,b）。在这一思想的启发下，爱尔兰数学家哈密顿构造出了一种新数——四元数。简单地说，四元数是一种形如a+bi+cj+dk的数，这里a,b，c,d是实数，i,j，k是单位元，且i,j，k是满足i2=j2=k2=-1的虚数，同时i,j，k在相乘时必须满足以下规则：ij=-ji=k, jk=-kj=i, ki=-ik=j。四元数的加法与乘法也有系统的定义，与实数乘法不一样的是四元数的乘法不满足交换律。四元数的创立拓展了数的概念，深化了对运算法则的认识，使数学家意识到可以创造出有意义的新数作为数学研究对象。
【微问题】你能用欧拉公式推导出三角公式吗？
【关键词】复数 复平面虚数