大家知道，一个圆周角为360°。但为什么一个圆周角规定为360°呢？这和古人对世界的认识有关。古人认为1年有360天，而太阳在天空中的视直径，恰好是天球视周长的1/360，也就是说用360个太阳（人们看到的太阳）一个挨着一个紧紧排列，恰好就是一圈，所以就定义一圈是360°。虽然这种说法的根据是不科学的，但这种规定却被延续下来，其根源在于数字360本身有独特的性质：它拥有24个因数，容易被整除，在1～10中，除了7以外，其他自然数都是它的因数，所以对圆周角进行等分时有20多种情况都会得到整数角度。
采用圆周角为360°的角度制，确实为人们直观认识角度以及等分角度带来许多方便，但在真正去刻画圆的周长与面积时就难免产生不便。比如，把圆周角360°等分6份后，每份60°，60°的圆心角所对应的弦长正好等于半径，这一点很奇妙，也很有价值。但是，这种60对1的对应未免有些牵强，于是，瑞士数学家欧拉于1748年引入弧度的概念，他把半径为1的单位圆周上长度为1的弧所对的圆心角的大小定义为1弧度，这就是弧度制。
量角器
由于半径为1的圆周周长为2π，因此，在弧度制下，一个周角的大小就等于2π，而一个平角的大小正好是圆周率。由于在欧氏几何中，任何三角形的三内角之和都是一平角，这样用弧度来描述就变成：三角形三内角之和等于圆周率π。但也正因为如此，有不少人难以理解用弧度来度量角。这大概是因为通常给出一个度量时，一般总是将一个整体划分成整数份，比如将一天划分成24小时，将温度从冰点到沸点划分成100℃，等等。将一个平角划分成180°和我们通常的概念相同，因而容易接受。而π不是整数，甚至不是有理数，将一个平角划分成π份不太容易接受，但这并不影响用弧度来度量一个角度的大小。事实上，我们可以将一个平角的大小设为1，而任何一个角度可以和平角进行比较，比如30°的角是1/6个平角，因此可以认为30°的角的大小是1/6，而弧度只是再乘上一个π而已。
弧度制和通常的角度表示相比有许多优点。在弧度制下，角的度量值无需转化就直接与弧长挂钩，即有角度
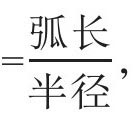这在实际测量、计算角量（角速度、角加速度）等时都带来方便。比如，对于一个扇形，假如其半径为l，扇形的角度（弧度）为θ，那么，这个扇形的弧长就是s=lθ，而面积则为
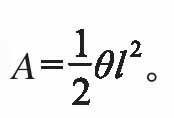现代数学一般都用弧度作为角的单位，在微积分中研究量的变化关系时，都采用弧度制。容易看出一个圆心角在单位圆周上所对的弧长和弦长之比，随着角度越来越小而越来越接近于1，而在弧度制下，弧长等于角度，用高等数学极限论的语言写出来就是
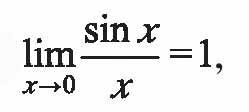这使数学公式变得简洁而优美。比如欧拉公式eiπ+1=0，它将0，1，π，e, i这5个最重要的数学常数用一个简明的公式建立起了联系，被称为最美的数学公式，这里的π就是弧度制下的平角。如果没有弧度制，这样优美的数学公式将不复存在。（张文俊）