^*牛顿(Newton)和^*莱布尼兹(Leibniz)首创的数学技术，基于连续变化量中无限小变化的概念。例如，微积分用于把一个运动中的物体的速度定义为该物体在任一时刻位置的变化率。速度(v)称为位置(x)相对于时间(t)的导数;在微积分中记作v=dx/dt。式中dt为小得趋于零的时间间隔，dx为物体在这一时间中所走的距离。若x是t的一个已知函数，则可以通过计算(微分运算)这一函数相对于时间的导数而求得v在任一时刻的值。同样，任一时刻速度的导数(或位置的二阶导数)给出它的加速度(a)，亦即d²x/dt²＝dv/dt=a。微分学是进行这种运算的规则系统。在图表上，函数的导数是任意一点上曲线的斜率。函数的最大值或最小值可以求出，因为它们出现于斜率为零的时候。积分学研究其逆过程。若速度是时间的连续变化函数，算出组成该时间间隔的每一个无限小时间间隔(dt)的v和dt的积所构成的和，则得到在适当一段时间间隔中位置的变化。积分的求解遵循一般规则，每种函数有一个相应的积分。时间t₁和t₂之间v的积分记作

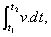
表示这一时间间隔中位置的变化。在图表上，函数曲线和水平轴之间的面积是特定间隔中函数的积分。

包含导数的方程式称为微分方程式。其求解过程是推测一个一般形式的解，并以微分规则代入式中检验。