有些作物，特别是果树，会出现一年高产（俗称大年）、一年低产（俗称小年），并且大小年交替发生的现象。为什么会出现大小年现象呢？抛开生物原理不谈，我们可以将它归结为一个数学模型，用数学原理来解释。
马尔萨斯
先从关于生物种群增长的马尔萨斯模型谈起。英国牧师马尔萨斯在其1798年发表的《人口学原理》中指出：人口是以几何级数增长的，即某一年的人口增量与上一年人口基数成比例。用数学公式可以写成：如果记第n年的人口为xn，则第n+1年的人口为xn+1=rxn，这里r是一个正的比例常数。马尔萨斯指出，该模型对所有生物种群都适用，即xn也可以是生物种群的个体数量。此模型在预测人口和生物种群的增长时曾起过一定作用，但也存在一个问题：在r＞1时，随着时间n的增加，种群中个体数量将会以指数方式无限增长，这显然是不符合实际的，因为在种群所生活的环境里资源总是有限的，任何种群都不可能无限制增长。事实上，马尔萨斯模型仅仅对种群较小或者种群生长所需资源极为丰富的情况下才适用。为了使这一模型更加符合实际，可以对马尔萨斯模型做一个修正，首先假设在特定环境下，种群可能的最大生存数量有一个上限M。其次，种群增长率不应是常数，而是随着种群的增大而减小直至不再增长。在这样的假设下，马尔萨斯模型可修正为xn+1=rxn（M-xn），归一化（即不妨设M=1）后的模型为
xn+1=rxn（1-xn），
此时xn的数值在0～1之间。这一模型称为逻辑斯蒂生长模型，很多生物种群的生长系统均符合这一模型。研究发现，尽管这一模型看起来很简单，但其动力学行为却非常复杂。为说明这一点，我们可以按照参数变化情况，来观察这一模型：
当参数r在0和1之间时，xn会随着n增大而越来越小，并最终趋向于0，也就是出现了负增长，种群将逐渐变小直至消失。
当r在1和2之间时，xn逐渐增长并趋于稳定，即种群逐年增大并最终达到一个稳定的状态。
当r在2和3之间时，xn也会最终趋于一个稳定值，但不是逐渐增大，而是以上下波动的方式逐渐趋于这个稳定值。
而当r在3和3.45之间时，情况又不同了，xn会交替地趋于两个不同的稳定值，并在这两个稳定值之间循环震荡，即xn趋于一个2周期循环。反映在种群生长上，就出现了种群一年大、一年小，并且交替发生的现象。
要是r继续增大呢？情况会更复杂些，当r在3.45～3.54之间，xn会轮流趋向于4个不同的稳定值，即趋向于一个4周期循环。随着r继续增大，xn还会依次趋向于8周期循环、16周期循环、32周期循环……这种现象称为逻辑斯蒂模型的倍周期现象。
当r增大到大约3.57时，情况将变得极为复杂。此时，xn的状态基本上不会稳定于任何周期循环，其取值看上去是无序而没有规律的。并且，如果一开始的初值x1有一个细微的变化，随着时间n的增加，xn的变化都将会被放大而产生明显的差异。这种现象就称为混沌，或者说整个系统处于混沌状态。
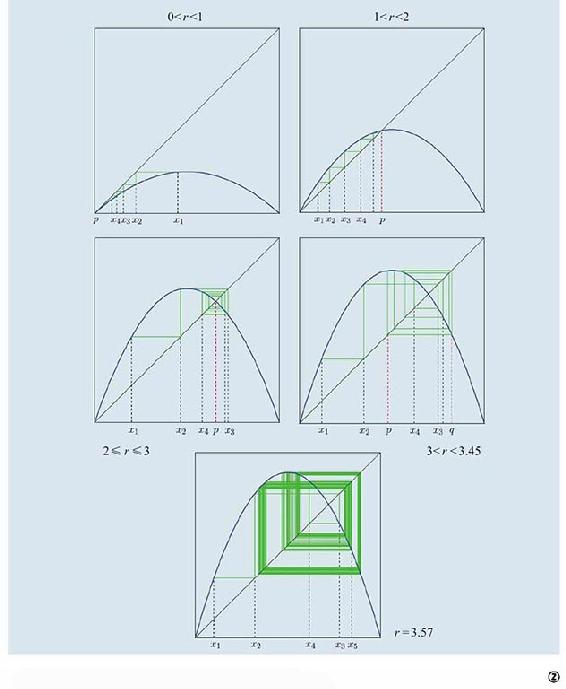
逻辑斯蒂模型在各种参数下xn的变化情况
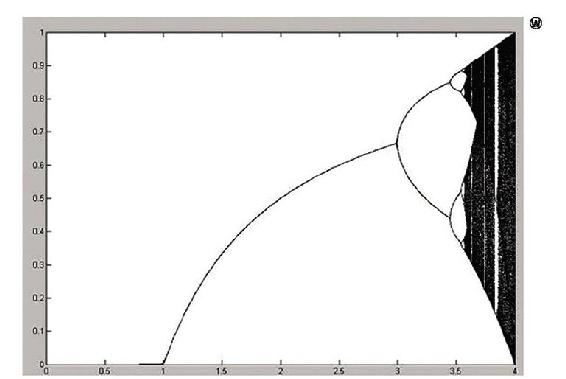
逻辑斯蒂模型分叉图，随着r的增加，其最终状态从1个稳定值分化到2个、4个、8个……周期稳定值，并在r=3，3.45，3.54，……处产生分叉。图中右端黑色区域表明系统处于混沌状态，没有周期稳定态。图中还可以看到，在r=3.83左右有一个白色的“窗口”，此时系统不再混沌而是变得有序，它会稳定于一个3周期循环
那为什么逻辑斯蒂模型会这么复杂呢？逻辑斯蒂模型可以重写为xn+1=rxn-rxn2，和马尔萨斯模型比较，我们发现马尔萨斯模型右端只有一次项，这种模型称为线性模型，其动力学行为比较简单。而逻辑斯蒂模型多了一个xn的平方项，这是一个非线性项，所以逻辑斯蒂模型是一个非线性模型，而正是这个非线性项，导致了逻辑斯蒂模型的复杂动力学行为。基本上所有的非线性系统都是非常复杂的，而现实世界中的大多数系统都是非线性的，因此，非线性科学已成为现代科学研究中极为重要的领域。
农林作物也是生物种群，一些作物的生长也符合逻辑斯蒂模型，如果其符合的逻辑斯蒂模型的参数r在1～3之间，则在若干年后会有稳定的产量。如果参数r的数值恰好落在3～3.45之间，就会出现一年高产、一年低产并且交替发生的大小年现象，这就是大小年现象的一种数学解释。
大小年现象不利于作物的高产稳产，通常可以通过修剪、加强肥水管理等科学种植技术来改变作物生长所符合的逻辑斯蒂模型中的参数，从而达到弱化大小年现象甚至让大小年现象消失的目的。（邱维元）
【微问题】为什么科学种植可以改变逻辑斯蒂模型的参数？
【关键词】数学模型 动力系统
- 为什么含羞草的叶子一触即合？
- 为什么听到楼上玻璃珠掉地上
- 为什么吸尘器能吸尘?
- 为什么吸尘器能除尘?
- 为什么吸烟会导致脑机能衰退?
- 为什么吸烟有害健康?
- 为什么吸管可以吸上饮料来?
- 为什么吸血的总是雌蚊子
- 为什么吸进空气呼出的却是二氧化碳
- 为什么吹电风扇和扇扇子会使人感到凉快些
- 为什么吼猴特别爱吼叫
- 为什么吼猴的叫声很洪亮
- 为什么吼猴的叫声特别响?
- 为什么周幽王要烽火戏诸侯?
- 为什么味精生产要用谷氨酸棒杆菌
- 为什么和恐龙同时代的一些其他生物没有灭绝
- 为什么咸鸭蛋会出油?
- 为什么哈雷彗星能准时回归?
- 为什么响尾蛇的尾巴会发声
- 为什么响尾蛇的尾巴会响?
- 为什么响尾蛇的尾巴会响
- 为什么哥伦布会把美洲当作印度
- 为什么哺乳动物在新生代占据了主导地位？
- 为什么哺乳动物的眼睛有些长在脸正前方,有些长在脸两侧
- 为什么哺乳动物的眼睛要长在前面