毕达哥拉斯
公元前6世纪的一天，古希腊数学家毕达哥拉斯走过一个铁匠铺，听到锤子敲打着铁块，发出悦耳的和声。于是，他跑进铁匠铺对锤子进行分析，认识到那些彼此音调和谐的锤子有一种简单的数学关系——它们的质量相互之间成简单比。具体点说，那些重量等于某一把锤子重量的1/2，1/3，1/4的锤子都能产生和谐的声响。另一方面，那把和任何别的锤子一起敲打时总发出噪声的锤子，它的重量和别的锤子的重量之间不存在这种简单整数比关系。
毕达哥拉斯在琴弦上重复了这一试验，并得出相同的发现：当琴弦被分成的两段长度是简单整数之比时，琴弦能发出更好听的音调。音调的和谐竟由整数的比决定！来自音乐的这一发现给毕达哥拉斯很大的启迪。后来，他把行星的运动也归结为整数的比。
一幅木刻作品中的毕达哥拉斯，正在探讨数与音乐的关系
毕达哥拉斯在这些发现的基础上宣称：万物皆数，即整个世界都可以用整数或整数的比来解释。这成为他及其领导的毕达哥拉斯学派的信条。
他们的这一观念体现在几何中就是：任何两条线段都是可公度的。这里先对这个陌生的概念解释一下。设两条线段长度分别是a与b，如果可以找到一条长度为d的小线段，使a可以分成d的某整数倍，比如n倍，即a=nd；同时使b可以分成d的另一整数倍，比如m倍，即b=md，此时，就称线段a与b是可公约或可公度的（d就是两者的共同度量单位）。事实上，用我们熟悉的语言表述就是，任意两条线段长度之比是整数或是一个分数。
这一非常符合常识与直觉的结论，似乎是无可怀疑的，而且在当时也被古希腊人所普遍接受。转折是从毕达哥拉斯证明勾股定理后开始的。毕达哥拉斯的一个学生希帕索斯在研究老师的著名成果时，想到这样一个问题：正方形的对角线与边长这两条线段是不是可公度的呢？经过认真的思考，希帕索斯意外地发现这两条线段不存在共同的度量单位：不管度量单位取得多小，都不可能成为正方形的边与对角线的共同度量单位。一句话，正方形的边和对角线是不可公度的！或者说，正方形对角线与边长的比（即我们所熟知的
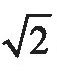）既不是一个整数，也不是分数，而是一个当时人们完全不了解的全新的数。这一发现对毕达哥拉斯及其学派来说完全是致命的，它彻底推翻了他们的数学与哲学信条。据传说，希帕索斯因为把发现泄漏出去，而被毕达哥拉斯的信徒扔进大海里淹死了。
在希帕索斯之后，人们发现了许多与
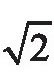一样的数。后来，这类数被统称为“无理数”，与之相对，人们原来接受的数（整数或整数的比）被称为“有理数”。而“有理”与“无理”的术语在古希腊人那里原意是指“可比的”与“不可比的”。在后来转译的过程中，在“可比的”这个含义之外，派生出“有理（合乎情理）”与“无理（不合情理）”的含义。再后来，中国在转译时就将其译成了“有理数”和“无理数”，大家也就不太知道它们原来的意思是“可比数”与“不可比数”了。（韩雪涛）【微博士】第一次数学危机
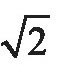的出现在古希腊数学界掀起了一场巨大风暴，直接动摇了毕达哥拉斯学派的数学信仰，引发了西方数学史上一场大风波，史称“第一次数学危机”。第一次数学危机表明，几何量不能完全由整数及其比来表示，反之，数却可以由几何量表示出来。整数的尊崇地位受到了挑战，古希腊人的数学观念受到极大的冲击。从此，几何学开始在古希腊数学中占有特殊地位。人们如果遇到二次方程或别的代数问题中出现无理数，就把它变为一个几何问题进行处理。- 蜂巢里有些什么存在
- 蜂巢里有什么
- 蜂王用什么来号召蜜蜂大军
- 蜂蟹为什么会不停地吐泡泡?
- 蜂鸟有什么特别飞行绝技
- 蜂鸟的飞行速度有多快？
- 蜂鸟的飞行速度有多快？能够迁徙多远？
- 蜂鸟翅膀振动的速度有多快？
- 蜈蚣到底长多少只脚?
- 蜈蚣有那么多脚，为什么不会被自己绊倒
- 蜈蚣真有100条腿？千足虫有1000多条腿吗？
- 蜗牛和蛞蝓为什么会留下闪亮的足迹?
- 蜗牛喜欢吃什么东西?
- 蜗牛是如何爬行的?
- 蜗牛爬行时为何会留下“足迹"
- 蜗牛爬过的地方为什么会有一条涎线
- 蜗牛的壳有什么用?
- 蜗牛的速度有多快？
- 蜘蛛丝为什么那么坚韧
- 松狮犬被主人带去剪了一个霸气的发型
- 松红梅是怎样养殖的呢
- 松脂是什么？
- 松露是什么？
- 松露长什么样？
- 松香是什么？