对于大多数人来说，“整体大于部分”是一个天经地义、不容争辩的事实。古希腊数学家欧几里得还将它作为一个公理写进《几何原本》之中。现在如果有人告诉你，整体和它的部分在数量上有可能一样多，你是否会感到很惊讶？
为了解释清楚这个问题，我们先来考虑说两种事物数量上一样多是怎么一回事。假设在文艺演出的现场我们看到座无虚席，而且没有人站着，那么不必去数座位数和人数，就可以知道它们是一样多的。这是因为座位和人之间可以实现一一对应。抽象地说就是：如果两个集合之间可以建立起一一对应的话，那么它们的元素个数是相等的。显然，一个有限集合是没有办法和它的一部分建立起一一对应的。但无穷集合的情况会是怎样呢？
剧场里座位与人之间一一对应
1638年，意大利物理学家伽利略在他的书中记录了如下令他吃惊的事实：
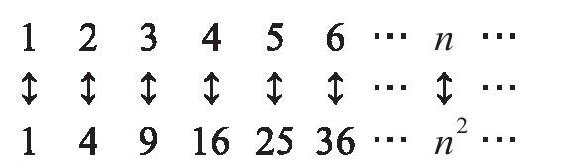
这表明每个正整数都和它的平方数一一对应，因此平方数和正整数一样多。但平方数只是正整数的一部分，所以正整数可以和它的部分一样多。
波尔查诺
伽利略的发现在当时并没有引起人们的注意。200年后，一位名叫波尔查诺的捷克数学家又重新指出了同样的事实，而且更为一般：一个无穷集合可以和它的真子集作成一一对应。但这次仍然没有引起广泛注意。直到1872年以后，德国数学家康托尔才真正开始了对于无穷集合的深入研究。康托尔确信，一个集合能够和它的真子集大小相等正是无穷集合的本质特征。不但如此，他还发现关于无穷集合会有更多人们想象不到的事情发生。（李文林 程钊）
【微问题】两个代数数之和是否还是代数数？
【关键词】代数数 超越数
- 为什么昆明被称为"春城"?
- 为什么昆虫会蜕皮?
- 为什么昆虫没有鼻子却嗅觉灵敏?
- 为什么昆虫的眼睛里有成千上万个镜头？
- 为什么明式家具会受到现代人的喜爱
- 为什么昙花在夜晚开放?
- 为什么昙花开花时间非常短?
- 为什么昙花的开花时间很短?
- 为什么星巴克横着排队麦当劳竖着排队?
- 为什么星星之火，可以燎原
- 为什么星星会一闪一闪的?
- 为什么星星会眨眼睛?
- 为什么星星会闪烁？
- 为什么星星大多是球形的?
- 为什么星星有不同的颜色?
- 为什么星星有名字?
- 为什么星星有的亮,有的暗
- 为什么星球大多是球体?
- 为什么星系也爱抱成团
- 为什么星系会发生碰撞和并合
- 为什么春天人容易困倦
- 为什么春天会飞出许多“白毛毛"
- 为什么春天里人会感到困倦
- 为什么春秋季节容易发生哮喘
- 为什么春节又叫过年春节又叫过年的原因