分数（包括整数）是有理数，从小数的角度看，就是有限小数或者无限循环小数。这意味着，分数与有限小数或无限循环小数之间，是可以互相转化的。为什么呢？
一个分数
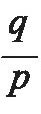的值，也就是用p去除q所得的值。用p去除q，每一次的余数只可能是0或1，2，…，p-1等p种情况。如果某次的余数是0，则得到的商就是有限小数；如果余数始终不为0，那么余数只有p-1种情况，按照抽屉原则，商的小数点后p位小数的余数中必有两位是重复的，因此必然在重复余数后造成循环，也就是说得到的商是无限循环小数，而且其第一个“循环节”必然在前p位小数内开始。因此，分数可以转化为有限小数或无限循环小数。反过来，有限小数或无限循环小数也可以化为分数。有限小数转化为分数是简单的，一个具有n位小数的有理数，只要将其放大10n倍，再除以10n即可。例如
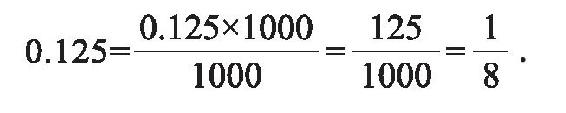
对于无限循环小数，则可先将该小数分别放大10n+m倍和10n倍，其中n是小数的非循环部分的位数，m是一个循环节的位数。这两个放大后的数其小数部分将完全相同，相减就得到一个整数。从而就可将原小数化为分数。例如：对a=0.24126126126…，小数点后前两位24是非循环部分，循环节为126，有3位。计算
100000a=24126. 126126…，
100a=24. 126126126….
相减得到（100000a-100a）=24126-24=24102。于是
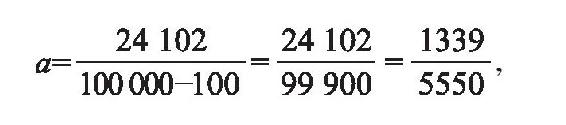
我们就将无限循环小数a化为了分数。
（张文俊）