代数问题的求解通常是比较规范的，按照一定的步骤依葫芦画瓢即可，关键是计算不出错；而几何则不同，难度稍大的题目，往往无从下手，好似羚羊挂角，无迹可寻。辅助线从何而来，要么是妙手偶得之，要么是千锤百炼的反应。人通过推理，可以由此及彼，由表及里，去粗取精，去伪存真。那么，为计算而发明的计算机，能够求解几何题目吗？
事实上，计算机可供解题使用的基本功能，大体上就可分为4类：变量赋值，基本运算，条件选择，循环操作。计算机要想解题首先要记得住东西，不仅要记住解题的有关知识和方法，还要能表达出来。要求计算机既能记住我们要它记住的信息，又能表达出来，这种功能主要通过变量赋值来实现。
除了能记住东西，还要会做基本的运算。计算机做计算肯定是不成问题的，否则怎么叫计算机呢？不过我们这里所讲的计算，除了包含一般所说的数值计算，还包括符号计算功能。因为数值运算通常容易出现误差，多步推导之后，误差被积累，可能导致结果谬以千里。在求解问题时，要根据不同的情形使用不同的公式和方法，而几何问题的条件千差万别，计算机可以根据条件安排，自动区别不同的情形，执行不同的运算，这就用到了条件选择的功能。
计算机的另一长处就是不怕枯燥麻烦。一个运算或一套操作，让它重复多少次它也不会罢工或埋怨。几何问题有时要多次检验，有时要反复探索，有时又要做大量演算。只要你一声令下，它就老老实实干起来，直到完成预定次数或达到某个目标。这叫作循环操作功能。
几何题有计算题、证明题，还有作图题。它们各有特点，又是相通的。两千多年来，人们积累了丰富多彩的解几何题的经验、技巧和方法。这些有待教给计算机的解题本领，大体可以分为4类：检验、搜索、归约和转换。
要问计算机如何解几何题，就得先看人如何解几何题。以几何学家为例，如果他们拿到一个几何题，有哪些高招呢？首先，要画画看看，量量算算，看题目出得对不对，合理不合理。不合理就不做下去了。这叫作检验。然后，根据条件，参照问题，能试着东推推，西试试，推出来的东西有用没用先记下来。这样或许能解决问题，如果解决不了，再想别的出路。说不定记下来的材料还有用。这叫搜索。如果搜索不出来，还可以抓住问题的目标（待证的结论、待求的几何量或待作的点与线），分析计算，化简条件，消去中间的参数或几何元素，力求水落石出。这叫归约。
当上述常规的方法不能奏效时，人的智慧和灵感就成为取胜的源泉了。或用反证法、同一法，或加辅助线，或对部分图形作平移旋转，总之是改变问题的形式，以求化繁为简。这叫转换。
人们解几何问题的招数，层出不穷，争奇斗艳。概括起来，不外乎这4类：检验、搜索、归约和转换。多年以来，数学家和计算机科学家费尽心思，循循善诱，把个中奥秘向计算机传授。使得计算机解几何题的能力日新月异，大放光彩。除了灵机一动加辅助线，或千变万化的问题转换之外，前3种办法计算机都学得十分出色了。用计算机帮助学者研究几何，帮助以至代替老师指导学生学习几何，已经从古老的梦想变为现实。
几何专家解题的过程也给计算机提供了榜样。
在解题之前，计算机必须先要掌握有关的几何知识：公理、定理、定义、公式，我们称之为推理规则，也就是头脑里先得有一个知识库——推理规则库。读了题目之后，把题目提供的几何信息记在头脑里，这就形成了一个临时的几何信息库。然后计算机要进行“思考”，将知识库里的推理规则应用于几何信息库里的信息。推出了新信息，就把新信息和它的来历加到信息库里。虽然并不是每条新信息都有用。可是在题目还没完全解答出来的时候，天晓得哪条信息有用，哪条信息没有用，还是统统记下来为妙。
如果所有的推理规则都用了，还得不到新的信息，就到此为止，别干下去了。这表明几何信息库再也不能扩大了，叫作达到了推理不动点。这时，如果几何信息库中包含了所要求证的结论或待求的几何量，则解题成功。否则解题失败。
通常，需要随时关注新信息是不是包含了所要的结论。结论一出来，就不再去追求推理不动点。解题成功，就可以从你记下来的信息当中提取有关的东西，组织成一个有条有理的证明或解法。解题失败，并不意味着几何信息库就没用了。它可以作为你进一步思考的基础。进一步思考的方向有：要不要多学点几何知识，增加几条推理规则；要不要添加辅助线；要不要用同一法或反证法。
复杂的推理过程可以化为简单的机械化的操作，但简单的操作重复多次就不再简单了。许多几何问题包含了大量的信息。人在进行解题思考时能借助于直觉和经验，抓住最关键的信息得到解答，计算机却靠机械地搜索，工作量非同小可。譬如一个三角形和它的三条高线以及垂心，这是个很简单的几何图形，用计算机搜索几何信息，居然发现图中有105条组成比例的线段。
计算机在搜索中得到的有用信息很多，而没用的信息更多。大量的操作才能从许多无用的信息中寻找出有用的结论，难度就好比沙里淘金。这种一网打尽、竭泽而渔的搜索推理，并不是什么新的发现，而是一种古老的机械化推理设想。在没有计算机的时代，也只能想想而已，一旦有了计算机，科学家就希望将之付诸实践，但困难的是难以将这个一般性的想法实现为有效的算法和程序。现在，这个梦想已经成为生活中的现实。这个成功来之不易，这是许多科学家多年努力的成果。其中，当代中国科学家的工作起了决定性的作用。（张景中 彭翕成）
【微博士】五点共圆问题的机器证明
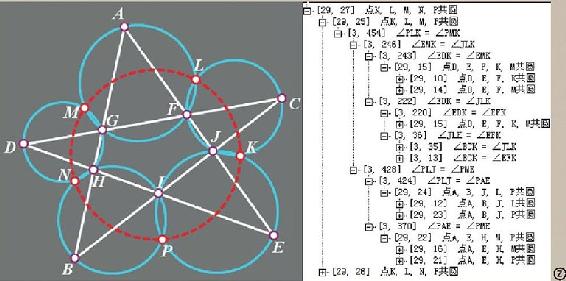
如图，作五角星ABCDE，产生5个交点G、H、I、J、F；再分别作△AGF、△DHG、△BIH、△EJI、△CFJ的外接圆；这5个圆生成5个新的交点M、N、P、K、L；求证：M、N、P、K、L五点共圆。超级画板自动推理只需2.9秒，图为部分推理过程。
【微问题】中国数学家在机器证明领域有哪些研究成果？
【关键词】机器证明 数学推理