如果让你计算4199710.4828+2.1829765,估计你用不了一分钟就能算好(加上检验),如果是4199710.4828×2.1829765呢?甚至更恐怖的4199710.48282.1829765呢?你可能会拿起计算器算个不停,如不允许使用计算器,你肯定会表示抗议,因为这实在太“摧残人”了!如果计算是无法想象的41997104.8282 1.829765,你肯定会想,难道出题人疯了?
可是你知道吗?历史上,早在计算器发明之前,欧洲的数学家和天文学家就遇到了大量棘手的计算问题,这些计算也就是与上述数字差不多的四则运算和幂、根号运算。这些烦人的计算不知耗费了多少人多少的时间和精力。于是,自然有人会想,有没有办法改进计算呢?终于,有人想出了奇妙的办法,这就是对数的由来。
对数运算是指数运算的逆运算。对数的发明者纳皮尔考察了两组数列,当第一组数列按等差数列增加,而第二组数列按等比数列增加时,后一组每两个数的乘积关系与前一组数中对应的两数之和,建立了一种简单的对应关系,由此就有了对数思想的萌芽。酝酿多年之后,纳皮尔出版了自己的著作,对数就开始传播开来。多位数学家为编制对数表付出了艰辛的努力,为人类文明做出了不可磨灭的贡献。
有了对数,就可将乘除运算转化为加减运算,即
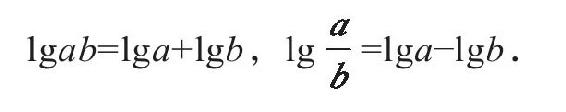
比如,当我们要计算9710.3265÷2.1829(这两个数被称为真数)时,我们就取它的对数,通过对数表查出lg9710.3265=3.9872和lg2.1829=0.3390,把它们相减得到3.6482,再查反对数表,就可求出9710.3265÷2.1829的值4448.3607。上面求出的值是近似值,但只要对数表足够精确,误差可以很小,对于一般的计算也足够精确了。
同样道理,通过对数可以把幂运算转换成乘法运算,即lgab=blga。如果你还嫌乘法复杂,还可以再通过对数把乘法变成加法,然后通过反对数表逐一求回去,直到得出正确的解答。
因此,对数的发明不愧是数学方法上的一次重大革新,这对当时日益繁重的科学计算是一个极大的改进。或许有人会说,现在有了电子计算机,人们做复杂运算已不再需要查对数表了。但别忘了,对数和对数函数也是数学本身的一个重大创造,在数学理论和自然科学中到处有它们永恒的身影。法国著名数学家拉普拉斯说,“对数的发现延长了天文学家的寿命。”伽利略则感叹:“给我空间、时间和对数,我可以创造出一个宇宙来。”(田廷彦)

对数的发现延长了天文学家的寿命