火腿三明治的标准配置是两片面包夹上一片火腿和一片奶酪。如果把这些配料对齐，然后一刀平分所有配料，这似乎并不是一件十分困难的事（如不计误差）。但如果三明治夹得歪歪扭扭，还能不能一刀平分呢？
火腿三明治很厚，给它切一刀属于立体几何的范畴，先考虑平面上类似的情况可能更明智：假设在桌面上放了一片火腿和一片奶酪，能只切一刀就把它们同时平分吗？如果桌面上放的是两块比萨饼的话，这个任务轻而易举，只要沿着通过两块比萨饼圆心的直线，一刀就能解决问题。但火腿和奶酪都不是规则的几何图形，问题似乎并不那么简单。
我们先来考虑更简单的问题：如何一刀把一个任意的有界几何图形分成面积相等的两部分？这似乎不困难，对于一个几何图形S，我们取从两边夹住它的一对平行线l1和l2。如果我们将另一条直线l从l1连续地平行移动到l2的话，整个过程中S从直线l的一边跑到了另一边。因为整个过程是连续的，所以必定有某个时刻，直线l恰好平分图形S的面积，这就是那一刀要切的位置。我们注意到，无论平行线指向什么方向，这个证明都是有效的。也就是说，即使我们指定直线的方向，也总能找到能平分图形的直线。但指定方向之后，能平分图形的直线就是唯一的了。
现在，我们尝试同时平分两个图形。先画一个能把两个图形S1、S2包起来的圆，假设它的圆心是O。在圆上任取一点P，根据刚才的论证，我们能找到直线l1、l2，它们分别平分S1、S2，而且同时与OP垂直。如果两条直线重合，那么我们就找到了一刀同时平分两个图形的办法。否则，直线l1和l2与点P的距离一定不相同。不妨假设直线l1与点P的距离比较小。我们把点P的初始位置记下来，称为点Q，然后将点P慢慢沿着整个圆挪动。随着点P的连续运动，相应地l1和l2与点P的距离也连续变化着。当点P运动到圆上与起点Q正相对的地方时，PQ恰好是圆的直径，而这时对应的l1和l2也恰好是原来在点Q处的l1和l2。不同的是，现在l2与P的距离变得比l1要小了！因为两条直线和P的距离是连续变化的，所以在移动过程中必定有某个时刻，两条直线和P的距离相等，即3条直线重合。这时，沿着重合的位置一刀切开，恰好就能同时平分两个图形。
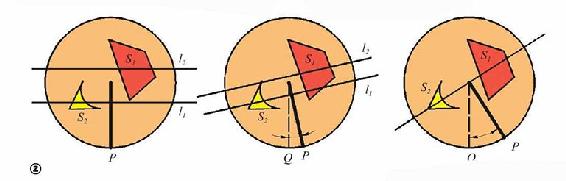
平分两个图形的方法示意图
在证明中，我们并没有考虑两个图形之间的关系。所以，这个结论除了可用到两片分开的火腿上，还可以用到煎蛋上：无论鸡蛋煎得怎么样，总能一刀把煎蛋切开，同时平分蛋黄和蛋白。类似的证明也可以推广到三维的情况，也就是对于任意三个三维立体，都可以沿着某个平面切一刀同时平分它们。这个结论有个有趣而形象的名称，就叫火腿三明治定理，看来数学家在聚餐时也是很讲究公平和效率的。
火腿三明治定理可以推广到更高的维度，但在更高维度上，无论是平面的面积还是立体的体积都失去了意义。在超过三维的空间里，需要一种叫作“测度”的数学对象进行高维形状之间的比较，它可以看成面积和体积的升级版。有关测度的数学理论叫作测度论，是数学中一门重要的分支，它不仅可以比较高维空间中形状的“大小”，也能“测量”在平面和三维空间中的某些奇怪形状（比如各种分形）的“面积”和“体积”。正因为广泛的适用性，测度论成为许多数学分支——比如数学分析和随机过程的基础。（方弦）
【微问题】为什么不能一刀平分三个比萨饼？
【关键词】毛球定理 切向量场 拓扑
- 所有的鸟都会飞吗？
- 所有细菌的形状都相同吗？
- 所有花儿都有香味吗？
- 所有行星上的1天都是24个小时吗？
- 扁形虫包括哪三种？
- 扁桃体发炎的注意事项有哪些
- 扁鹊为什么叫“神医"
- 扁鹊真有起死回生的本领吗
- 手为何会比脚灵活
- 手扎了为什么能马上收回来
- 手指为什么比脚趾长
- 手指甲和脚趾甲一样厚吗？
- 手指甲和脚趾甲的生长速度一样吗？
- 手指甲色泽判断健康
- 手指真的还能再造吗
- 手术后吃什么,不能吃什么?
- 手术后护士为什么总爱问患者放屁了没有
- 手机会危害人体健康吗？
- 手机信号微弱的时候还能拨打紧急电话吗
- 手机关机后睡觉是否有辐射
- 手机出现之前，人们在车中如何交流？
- 手机是如何工作的？
- 手机是怎么找到对方的
- 手机需要将电池用光之后再充电吗?
- 手枪为什么被称为是防身的最佳武器